



Next: NDFT - nonequispaced discrete
Up: NFFT 3.0 - Tutorial
Previous: Introduction
Contents
Notation, the NDFT, and the NFFT
This section summarises the mathematical theory and ideas behind the NFFT.
Let the torus
of dimension
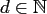 be given.
It will serve as domain from which the nonequispaced nodes
be given.
It will serve as domain from which the nonequispaced nodes
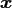 are taken.
Thus, the sampling set is given by
are taken.
Thus, the sampling set is given by
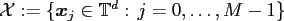 .
.
Possible frequencies
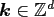 are collected in the multi-index set
are collected in the multi-index set
where
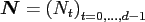 is the EVEN
multibandlimit, i.e.,
is the EVEN
multibandlimit, i.e.,
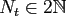 .
To keep notation simple, the multi-index
.
To keep notation simple, the multi-index
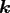 addresses elements of
vectors and matrices as well, i.e., the plain index
addresses elements of
vectors and matrices as well, i.e., the plain index
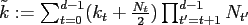 is not used here.
The inner product between the frequency index
is not used here.
The inner product between the frequency index
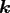 and the time/spatial
node
and the time/spatial
node
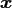 is defined in the usual way by
is defined in the usual way by
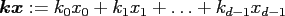 .
Furthermore, two vectors may be combined by the component-wise product
.
Furthermore, two vectors may be combined by the component-wise product
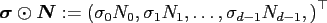 with its inverse
with its inverse
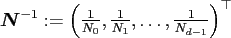 .
.
The space of all 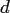 -variate, one-periodic functions
-variate, one-periodic functions
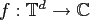 is restricted to the space of
is restricted to the space of 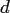 -variate trigonometric polynomials
-variate trigonometric polynomials
with degree
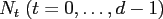 in the
in the 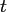 -th dimension.
The dimension
-th dimension.
The dimension
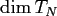 of the space of
of the space of 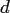 -variate trigonometric
polynomials
-variate trigonometric
polynomials 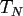 is given by
is given by
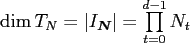 .
.
Subsections




Next: NDFT - nonequispaced discrete
Up: NFFT 3.0 - Tutorial
Previous: Introduction
Contents
Jens Keiner
2006-11-20
![]() are collected in the multi-index set
are collected in the multi-index set
![]() -variate, one-periodic functions
-variate, one-periodic functions
![]() is restricted to the space of
is restricted to the space of ![]() -variate trigonometric polynomials
-variate trigonometric polynomials