Dr. Manuel Gräf
Berechnungen
Dr. Manuel Gräf 

Spherical Designs


Degree t M Number of Points Oversampling Integration Error Gradient Norm Iterations Computation Time
49 1300 (random) 1.04 5.2e-12 9.2e-14 2211 3min
49 1300 (spiral) 1.04 1.7e-11 9.3e-14 7469 10min
50 1300 (random) 1.00 1.9e-5 8.8e-14 50212 1h
50 1300 (spiral) 1.00 6.8e-6 9.1e-14 96444 2h
100 5200 (random) 1.02 9.9e-12 9.8e-14 4211 27min
100 5200 (spiral) 1.02 1.6e-10 9.7e-14 57235 7.5h
200 21000 (random) 1.04 4.1e-12 9.9e-14 2597 1h
200 21000 (spiral) 1.04 1.0e-9 9.4e-14 173675 3d
500 130000 (random) 1.04 1.0e-11 9.9e-14 5394 21h
1000 520000 (random) 1.04 2.7e-11 1.3e-13 18000 17d
1000 1002000 (random) 2.00 9.7e-12 9.8e-14 4286 5d

The above table contains some examples of computed numerical spherical t-designs. The computation is based on the algorithms from [1] and utilizes the nonequispaced fast spherical Fourier transforms (NFSFT), which are implemented in the NFFT-library.
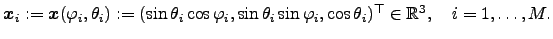
The text file for each point set consists of two columns which contain the spherical coordinates $ (\varphi,\theta) \in [0,2\pi] \times [0,\pi)$ of every point $ \boldsymbol x := \boldsymbol x(\varphi,\theta) := (\sin\theta \cos\varphi, \sin\theta \sin\varphi, \cos \theta)^{\top} \in \mathbb{R}^{3}.$

Bibliography

1
Gräf and D. Potts.
On the computation of spherical designs by a new optimization approach based on fast spherical Fourier transforms.
Numer. Math. 119, 699 - 724, 2011.