Introduction

Fast Fourier transforms (FFTs) belong to the '10 algorithms with the greatest influence on the development and practice of science and engineering in the 20th century'. The classic algorithm computes the discrete Fourier transform

$f_j= \sum_{k=-\frac{N}{2}}^{\frac{N}{2}-1} \hat{f}_{k} {\rm e}^{-2\pi{\rm i}\frac{kj}{N}}$

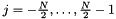for $j=-\frac{N}{2},\dots,\frac{N}{2}-1$ and given complex coefficients 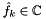$\hat{f}_{k}\in\mathbb{C}$ . Using a divide and conquer approach, the number of floating point operations is reduced from 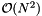${\cal O}(N^2)$ for a straightforward computation to only 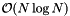${\cal O}(N\log N)$ . In conjunction with publicly available efficient implementations the fast Fourier transform has become of great importance in scientific computing.

However, two shortcomings of traditional schemes are the need for equispaced sampling and the restriction to the system of complex exponential functions. The NFFT is a C subroutine library for computing the nonequispaced discrete Fourier transform (NDFT) and its generalisations in one or more dimensions, of arbitrary input size, and of complex data.

More precisely, we collect the possible frequencies 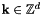$\mathbf{k}\in\mathbb{Z}^d$ in the multi-index set

$I_{\mathbf{N}} := \left\{ \mathbf{k}=\left(k_t\right)_{t=0,\dots,d-1} \in \mathbb{Z}^d: - \frac{N_t}{2} \le k_t < \frac{N_t}{2} ,\;t=0,\dots,d-1\right\},$

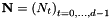where $\mathbf{N}=\left(N_t\right)_{t=0,\dots,d-1}$ is the multibandlimit, i.e., 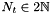$N_t\in 2\mathbb{N}$ . For a finite number of given Fourier coefficients 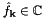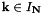$\hat f_{\mathbf{k}} \in \mathbb{C}$ , $\mathbf{k}\in I_{\mathbf{N}}$ , we consider the fast evaluation of the trigonometric polynomial

$f\left(\mathbf{x}\right) := \sum_{ \mathbf{k}\in I_{ N}} \hat{f}_{\mathbf{ k}} {\rm e}^{-2\pi{\rm i}\mathbf{k}\mathbf{ x}}$

at given nonequispaced nodes 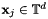$\mathbf{x}_j \in \mathbb{T}^d$ , $j=0,\ldots, M-1$ , from the 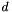$ d$ -dimensional torus as well as the adjoint problem, the fast evaluation of sums of the form

$\hat h_{\mathbf{k}} := \sum_{j=0}^{M-1} {f}_{j} {\rm e}^{2\pi{\rm i}\mathbf{k}\mathbf{ x}_j}.$

Generalisations

The generalisations of the NFFT include

NNFFT - nonequispaced in time and frequency fast Fourier transform,
NFCT/NFST - nonequispaced fast (co)sine transform,
NSFFT - nonequispaced sparse fast Fourier transform,
FPT - fast polynomial transform,
NFSFT - nonequispaced fast spherical Fourier transform.

Furthermore, we consider the inversion of the above transforms by iterative methods.

FAQ - Frequently Asked Questions

see https://www.tu-chemnitz.de/~potts/nfft/faq.php