 |
NFFT
3.4.1
|
 |
NFFT
3.4.1
|
This module implements nonuniform fast spherical Fourier transforms. More...
Data Structures | |
| struct | nfsft_wisdom |
| Wisdom structure. More... | |
| struct | nfsft_plan |
| data structure for an NFSFT (nonequispaced fast spherical Fourier transform) plan with double precision More... | |
Macros | |
| #define | NFSFT_NORMALIZED (1U << 0) |
| #define | NFSFT_USE_NDFT (1U << 1) |
| #define | NFSFT_USE_DPT (1U << 2) |
| #define | NFSFT_MALLOC_X (1U << 3) |
| #define | NFSFT_MALLOC_F_HAT (1U << 5) |
| #define | NFSFT_MALLOC_F (1U << 6) |
| #define | NFSFT_PRESERVE_F_HAT (1U << 7) |
| #define | NFSFT_PRESERVE_X (1U << 8) |
| #define | NFSFT_PRESERVE_F (1U << 9) |
| #define | NFSFT_DESTROY_F_HAT (1U << 10) |
| #define | NFSFT_DESTROY_X (1U << 11) |
| #define | NFSFT_DESTROY_F (1U << 12) |
| #define | NFSFT_NO_DIRECT_ALGORITHM (1U << 13) |
| #define | NFSFT_NO_FAST_ALGORITHM (1U << 14) |
| #define | NFSFT_ZERO_F_HAT (1U << 16) |
| #define | NFSFT_INDEX(k, n, plan) ((2*(plan)->N+2)*((plan)->N-n+1)+(plan)->N+k+1) |
| #define | NFSFT_F_HAT_SIZE(N) ((2*N+2)*(2*N+2)) |
| #define | BWEXP_MAX 10 |
| #define | BW_MAX 1024 |
| #define | ROW(k) (k*(wisdom.N_MAX+2)) |
| #define | ROWK(k) (k*(wisdom.N_MAX+2)+k) |
| #define | NFSFT_DEFAULT_NFFT_CUTOFF 6 |
| The default NFFT cutoff parameter. More... | |
| #define | NFSFT_DEFAULT_THRESHOLD 1000 |
| The default threshold for the FPT. More... | |
| #define | NFSFT_BREAK_EVEN 5 |
The break-even bandwidth 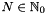 . More... . More... | |
Enumerations | |
| enum | bool { false = 0, true = 1 } |
Functions | |
| void | alpha_al_row (R *alpha, const int N, const int n) |
| void | beta_al_row (R *beta, const int N, const int n) |
| void | gamma_al_row (R *gamma, const int N, const int n) |
| void | alpha_al_all (R *alpha, const int N) |
Compute three-term-recurrence coefficients 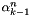 of associated Legendre functions for of associated Legendre functions for 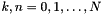 . More... . More... | |
| void | beta_al_all (R *beta, const int N) |
Compute three-term-recurrence coefficients 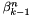 of associated Legendre functions for of associated Legendre functions for 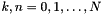 . More... . More... | |
| void | gamma_al_all (R *gamma, const int N) |
Compute three-term-recurrence coefficients 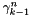 of associated Legendre functions for of associated Legendre functions for 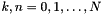 . More... . More... | |
| void | eval_al (R *x, R *y, const int size, const int k, R *alpha, R *beta, R *gamma) |
Evaluates an associated Legendre polynomials 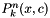 using the Clenshaw-algorithm. More... using the Clenshaw-algorithm. More... | |
| int | eval_al_thresh (R *x, R *y, const int size, const int k, R *alpha, R *beta, R *gamma, R threshold) |
Evaluates an associated Legendre polynomials 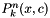 using the Clenshaw-algorithm if it no exceeds a given threshold. More... using the Clenshaw-algorithm if it no exceeds a given threshold. More... | |
| static void | c2e (nfsft_plan *plan) |
Converts coefficients 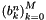 with with 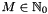 , , 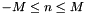 from a linear combination of Chebyshev polynomials from a linear combination of Chebyshev polynomials
to coefficients
for each order | |
| static void | c2e_transposed (nfsft_plan *plan) |
| Transposed version of the function c2e. More... | |
| void | nfsft_init (nfsft_plan *plan, int N, int M) |
| void | nfsft_init_advanced (nfsft_plan *plan, int N, int M, unsigned int flags) |
| void | nfsft_init_guru (nfsft_plan *plan, int N, int M, unsigned int flags, unsigned int nfft_flags, int nfft_cutoff) |
| void | nfsft_precompute (int N, double kappa, unsigned int nfsft_flags, unsigned int fpt_flags) |
| void | nfsft_forget (void) |
| void | nfsft_finalize (nfsft_plan *plan) |
| void | nfsft_trafo_direct (nfsft_plan *plan) |
| void | nfsft_adjoint_direct (nfsft_plan *plan) |
| void | nfsft_trafo (nfsft_plan *plan) |
| void | nfsft_adjoint (nfsft_plan *plan) |
| void | nfsft_precompute_x (nfsft_plan *plan) |
Variables | |
| static struct nfsft_wisdom | wisdom = {false,0U,-1,-1,0,0,0,0,0} |
| The global wisdom structure for precomputed data. More... | |
This module implements nonuniform fast spherical Fourier transforms.
In the following, we abbreviate the term "nonuniform fast spherical Fourier transform" by NFSFT.
This section summarises basic definitions and properties related to spherical Fourier transforms.
Every point in 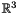 can be described in spherical coordinates by a vector
can be described in spherical coordinates by a vector 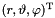 with the radius
with the radius 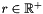 and two angles
and two angles ![$\vartheta \in [0,\pi]$](form_62.png) ,
, 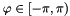 . We denote by
. We denote by 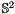 the two-dimensional unit sphere embedded into
the two-dimensional unit sphere embedded into 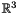 , i.e.
, i.e.
![\[ \mathbb{S}^2 := \left\{\mathbf{x} \in \mathbb{R}^{3}:\; \|\mathbf{x}\|_2=1\right\} \]](form_65.png)
and identify a point from 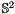 with the corresponding vector
with the corresponding vector 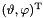 . The spherical coordinate system is illustrated in the following figure:
. The spherical coordinate system is illustrated in the following figure:
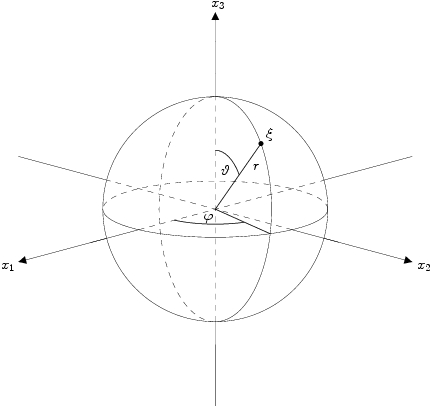
For consistency with the other modules and the conventions used there, we also use swapped scaled spherical coordinates 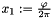 ,
, 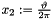 and identify a point from
and identify a point from 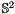 with the vector
with the vector ![$\mathbf{x} := \left(x_1,x_2\right) \in [-\frac{1}{2}, \frac{1}{2}) \times [0,\frac{1}{2}]$](form_69.png) .
.
The Legendre polynomials ![$P_k : [-1,1] \rightarrow \mathbb{R}$, $k \in \mathbb{N}_{0}$](form_70.png) as classical orthogonal polynomials are given by their corresponding Rodrigues formula
as classical orthogonal polynomials are given by their corresponding Rodrigues formula
![\[ P_k(t) := \frac{1}{2^k k!} \frac{\text{d}^k}{\text{d} t^k} \left(t^2-1\right)^k. \]](form_71.png)
The corresponding three-term recurrence relation is
![\[ (k+1)P_{k+1}(t) = (2k+1) x P_{k}(t) - k P_{k-1}(t) \quad (k \in \mathbb{N}_0). \]](form_72.png)
With
![\[ \left< f,g \right>_{\text{L}^2\left([-1,1]\right)} := \int_{-1}^{1} f(t) g(t) \text{d} t \]](form_73.png)
being the usual ![$\text{L}^2\left([-1,1]\right)$](form_74.png) inner product, the Legendre polynomials obey the orthogonality condition
inner product, the Legendre polynomials obey the orthogonality condition
![\[ \left< P_k,P_l \right>_{\text{L}^2\left([-1,1]\right)} = \frac{2}{2k+1} \delta_{k,l}. \]](form_75.png)
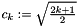 renders the scaled Legendre polynomials
renders the scaled Legendre polynomials 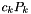 orthonormal with respect to the induced
orthonormal with respect to the induced ![$\text{L}^2\left([-1,1]\right)$](form_74.png) norm
norm
![\[ \|f\|_{\text{L}^2\left([-1,1]\right)} := \left(<f,f>_{\text{L}^2\left([-1,1]\right)}\right)^{1/2} = \left(\int_{-1}^{1} |f(t)|^2 \; \text{d} t\right)^{1/2}. \]](form_78.png)
The associated Legendre functions ![$P_k^n : [-1,1] \rightarrow \mathbb{R} $](form_79.png) ,
, 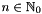 ,
, 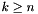 are defined by
are defined by
![\[ P_k^n(t) := \left(\frac{(k-n)!}{(k+n)!}\right)^{1/2} \left(1-t^2\right)^{n/2} \frac{\text{d}^n}{\text{d} t^n} P_k(t). \]](form_82.png)
For 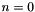 , they coincide with the Legendre polynomials, i.e.
, they coincide with the Legendre polynomials, i.e. 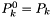 . The associated Legendre functions obey the three-term recurrence relation
. The associated Legendre functions obey the three-term recurrence relation
![\[ P_{k+1}^n(t) = v_{k}^n t P_k^n(t) + w_{k}^n P_{k-1}^n(t) \quad (k \ge n), \]](form_85.png)
with 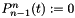 ,
, 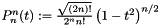 , and
, and
![\[ v_{k}^n := \frac{2k+1}{((k-n+1)(k+n+1))^{1/2}}\; ,\qquad w_{k}^n := - \frac{((k-n)(k+n))^{1/2}}{((k-n+1)(k+n+1))^{1/2}}. \]](form_88.png)
For fixed 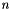 , the set
, the set 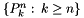 forms a complete set of orthogonal functions in
forms a complete set of orthogonal functions in ![$\text{L}^2\left([-1,1]\right)$](form_74.png) with
with
![\[ \left< P_k^n,P_l^n \right>_{\text{L}^2\left([-1,1]\right)} = \frac{2}{2k+1} \delta_{k,l} \quad (0 \le n \le k,l). \]](form_91.png)
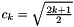 renders the scaled associated Legendre functions
renders the scaled associated Legendre functions 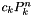 orthonormal with respect to the induced
orthonormal with respect to the induced ![$\text{L}^2\left([-1,1]\right)$](form_74.png) norm
norm
![\[ \|f\|_{\text{L}^2\left([-1,1]\right)} := \left(<f,f>_{\text{L}^2\left([-1,1]\right)}\right)^{1/2} = \left(\int_{-1}^{1} |f(t)|^2 \; \text{d} t\right)^{1/2}. \]](form_78.png)
The standard orthogonal basis of spherical harmonics for 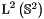 with yet unnormalised basis functions
with yet unnormalised basis functions 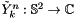 is given by
is given by
![\[ \tilde{Y}_k^n(\vartheta,\varphi) := P_k^{|n|}(\cos\vartheta) \mathrm{e}^{\mathrm{i} n \varphi} \]](form_96.png)
with the usual 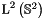 inner product
inner product
![\[ \left< f,g \right>_{\mathrm{L}^2\left(\mathbb{S}^2\right)} := \int_{\mathbb{S}^2} f(\vartheta,\varphi) \overline{g(\vartheta,\varphi)} \: \mathrm{d} \mathbf{\xi} := \int_{-\pi}^{\pi} \int_{0}^{\pi} f(\vartheta,\varphi) \overline{g(\vartheta,\varphi)} \sin \vartheta \; \mathrm{d} \vartheta \; \mathrm{d} \varphi. \]](form_98.png)
The normalisation constant 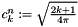 renders the scaled basis functions
renders the scaled basis functions
![\[ Y_k^n(\vartheta,\varphi) := c_k^n P_k^{|n|}(\cos\vartheta) \mathrm{e}^{\mathrm{i} n \varphi} \]](form_100.png)
orthonormal with respect to the induced 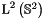 norm
norm
![\[ \|f\|_{\text{L}^2\left(\mathbb{S}^2\right)} = \left(<f,f>_{\text{L}^2\left(\mathbb{S}^2\right)}\right)^{1/2} = \left(\int_{-\pi}^{\pi} \int_{0}^{\pi} |f(\vartheta,\varphi)|^2 \sin \vartheta \; \mathrm{d} \vartheta \; \mathrm{d} \varphi\right)^{1/2}. \]](form_102.png)
A function 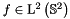 has the orthogonal expansion
has the orthogonal expansion
![\[ f = \sum_{k=0}^{\infty} \sum_{n=-k}^{k} \hat{f}(k,n) Y_k^n, \]](form_104.png)
where the coefficients 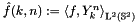 are the spherical Fourier coefficients and the equivalence is understood in the
are the spherical Fourier coefficients and the equivalence is understood in the 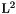 -sense.
-sense.
This section describes the input and output relation of the spherical Fourier transform algorithms and the layout of the corresponding plan structure.
The nonuniform discrete spherical Fourier transform (NDSFT) is defined as follows:
![\[ \begin{array}{rcl} \text{\textbf{Input}} & : & \text{coefficients } \hat{f}(k,n) \in \mathbb{C} \text{ for } k=0,\ldots,N,\;n=-k, \ldots,k,\; N \in \mathbb{N}_0,\\[1ex] & & \text{arbitrary nodes } \mathbf{x}(m) \in [-\frac{1}{2},\frac{1}{2}] \times [0,\frac{1}{2}] \text{ for } m=0,\ldots,M-1, M \in \mathbb{N}. \\[1ex] \text{\textbf{Task}} & : & \text{evaluate } f(m) := f\left( \mathbf{x}(m)\right) = \sum_{k=0}^N \sum_{n=-k}^k \hat{f}_k^n Y_k^n\left(\mathbf{x}(m)\right) \text{ for } m=0,\ldots,M-1. \\[1ex] \text{\textbf{Output}} & : & \text{coefficients } f(m) \in \mathbb{C} \text{ for } m=0,\ldots,M-1.\\ \end{array} \]](form_107.png)
The adjoint nonuniform discrete spherical Fourier transform (adjoint NDSFT) is defined as follows:
![\[ \begin{array}{rcl} \text{\textbf{Input}} & : & \text{coefficients } f(m) \in \mathbb{C} \text{ for } m=0,\ldots,M-1, M \in \mathbb{N},\\ & & \text{arbitrary nodes } \mathbf{x}(m) \in [-\frac{1}{2},\frac{1}{2}] \times [0,\frac{1}{2}] \text{ for } m=0,\ldots,M-1, N \in \mathbb{N}_0.\\[1ex] \text{\textbf{Task}} & : & \text{evaluate } \hat{f}(k,n) := \sum_{m=0}^{M-1} f(m) \overline{Y_k^n\left(\mathbf{x}(m)\right)}cd Do \text{ for } k=0,\ldots,N,\;n=-k,\ldots,k.\\[1ex] \text{\textbf{Output}} & : & \text{coefficients } \hat{f}(k,n) \in \mathbb{C} \text{ for } k=0,\ldots,N,\;n=-k,\ldots,k.\\[1ex] \end{array} \]](form_108.png)
This section describes the public layout of the nfsft_plan structure which contains all data for the computation of the aforementioned spherical Fourier transforms. The structure contains private (no read or write allowed), public read-only (only read access permitted), and public read-write (read and write access allowed) members. In the following, we indicate read and write access by read and write. The public members are structured as follows:
N_total (read) The total number of components in f_hat. If the bandwidth is 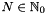 , the total number of components in
, the total number of components in f_hat is N_total 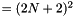 .
. M_total (read) the total number of samples 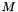
f_hat (read-write) The flattened array of spherical Fourier coefficents. The array has length 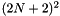 such that valid indices
such that valid indices 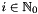 for array access
for array access f_hat 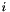
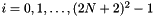 . However, only read and write access to indices corresponding to spherical Fourier coefficients
. However, only read and write access to indices corresponding to spherical Fourier coefficients 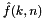 is defined. The index
is defined. The index 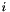 corresponding to the spherical Fourier coefficient
corresponding to the spherical Fourier coefficient 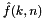 with
with 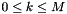 ,
, 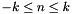 is
is 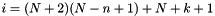 . For convenience, the helper macro NFSFT_INDEX(k,n) provides the necessary index calculations such that one can write
. For convenience, the helper macro NFSFT_INDEX(k,n) provides the necessary index calculations such that one can write f_hat[ NFSFT_INDEX( 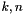
= 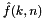 . The data layout is due to implementation details.
. The data layout is due to implementation details. f (read-write) the array of coefficients 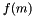 for
for  such that
such that f[ 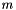
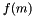
N (read) the bandwidth 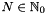
x the array of nodes ![$\mathbf{x}(m) \in [-\frac{1}{2},\frac{1}{2}] \times [0,\frac{1}{2}]$](form_124.png) for
for  such that
such that f[ 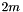
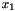 and
and f[ 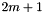
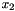
When using the routines of this module you should bear in mind the following:
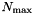 up to which precomputation is performed is always chosen as the next power of two with respect to the specified maximum bandwidth.
up to which precomputation is performed is always chosen as the next power of two with respect to the specified maximum bandwidth. f_hat while the input x is preserved. On the contrary, the adjoint NDSFT transforms (see nfsft_direct_adjoint, nfsft_adjoint) do not destroy the input f and x by default. The desired behaviour can be assured by using the NFSFT_PRESERVE_F_HAT, NFSFT_PRESERVE_X, NFSFT_PRESERVE_F and NFSFT_DESTROY_F_HAT, NFSFT_DESTROY_X, NFSFT_DESTROY_F flags. | #define NFSFT_NORMALIZED (1U << 0) |
By default, all computations are performed with respect to the unnormalized basis functions
![\[ \tilde{Y}_k^n(\vartheta,\varphi) = P_k^{|n|}(\cos\vartheta) \mathrm{e}^{\mathrm{i} n \varphi}. \]](form_138.png)
If this flag is set, all computations are carried out using the 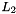 - normalized basis functions
- normalized basis functions
![\[ Y_k^n(\vartheta,\varphi) = \sqrt{\frac{2k+1}{4\pi}} P_k^{|n|}(\cos\vartheta) \mathrm{e}^{\mathrm{i} n \varphi}. \]](form_140.png)
Definition at line 575 of file nfft3.h.
Referenced by main(), nfsft_adjoint(), and nfsft_trafo().
| #define NFSFT_USE_NDFT (1U << 1) |
If this flag is set, the fast NFSFT algorithms (see nfsft_trafo, nfsft_adjoint) will use internally the exact but usually slower direct NDFT algorithm in favor of fast but approximative NFFT algorithm.
Definition at line 576 of file nfft3.h.
Referenced by main(), nfsft_adjoint(), and nfsft_trafo().
| #define NFSFT_USE_DPT (1U << 2) |
If this flag is set, the fast NFSFT algorithms (see nfsft_trafo, nfsft_adjoint) will use internally the usually slower direct DPT algorithm in favor of the fast FPT algorithm.
Definition at line 577 of file nfft3.h.
Referenced by main(), nfsft_adjoint(), and nfsft_trafo().
| #define NFSFT_MALLOC_X (1U << 3) |
If this flag is set, the init methods (see nfsft_init , nfsft_init_advanced , and nfsft_init_guru) will allocate memory and the method nfsft_finalize will free the array x for you. Otherwise, you have to assure by yourself that x points to an array of proper size before excuting a transform and you are responsible for freeing the corresponding memory before program termination.
Definition at line 578 of file nfft3.h.
Referenced by main(), nfsft_finalize(), and nfsft_init().
| #define NFSFT_MALLOC_F_HAT (1U << 5) |
If this flag is set, the init methods (see nfsft_init , nfsft_init_advanced , and nfsft_init_guru) will allocate memory and the method nfsft_finalize will free the array f_hat for you. Otherwise, you have to assure by yourself that f_hat points to an array of proper size before excuting a transform and you are responsible for freeing the corresponding memory before program termination.
Definition at line 579 of file nfft3.h.
Referenced by main(), nfsft_finalize(), and nfsft_init().
| #define NFSFT_MALLOC_F (1U << 6) |
If this flag is set, the init methods (see nfsft_init , nfsft_init_advanced , and nfsft_init_guru) will allocate memory and the method nfsft_finalize will free the array f for you. Otherwise, you have to assure by yourself that f points to an array of proper size before excuting a transform and you are responsible for freeing the corresponding memory before program termination.
Definition at line 580 of file nfft3.h.
Referenced by main(), nfsft_finalize(), and nfsft_init().
| #define NFSFT_PRESERVE_F_HAT (1U << 7) |
If this flag is set, it is guaranteed that during an execution of nfsft_direct_trafo or nfsft_trafo the content of f_hat remains unchanged.
Definition at line 581 of file nfft3.h.
Referenced by nfsft_finalize(), and nfsft_trafo().
| #define NFSFT_PRESERVE_X (1U << 8) |
If this flag is set, it is guaranteed that during an execution of nfsft_direct_trafo, nfsft_trafo or nfsft_direct_adjoint, nfsft_adjoint the content of x remains unchanged.
| #define NFSFT_PRESERVE_F (1U << 9) |
If this flag is set, it is guaranteed that during an execution of nfsft_direct_adjoint or nfsft_adjoint the content of f remains unchanged.
| #define NFSFT_DESTROY_F_HAT (1U << 10) |
If this flag is set, it is explicitely allowed that during an execution of nfsft_direct_trafo or nfsft_trafo the content of f_hat may be changed.
| #define NFSFT_DESTROY_X (1U << 11) |
If this flag is set, it is explicitely allowed that during an execution of nfsft_direct_trafo, nfsft_trafo or nfsft_direct_adjoint, nfsft_adjoint the content of x may be changed.
| #define NFSFT_DESTROY_F (1U << 12) |
If this flag is set, it is explicitely allowed that during an execution of nfsft_direct_adjoint or nfsft_adjoint the content of f may be changed.
| #define NFSFT_NO_DIRECT_ALGORITHM (1U << 13) |
If this flag is set, the transforms nfsft_direct_trafo and nfsft_direct_adjoint do not work. Setting this flag saves some memory for precomputed data.
Definition at line 589 of file nfft3.h.
Referenced by nfsft_forget(), and nfsft_precompute().
| #define NFSFT_NO_FAST_ALGORITHM (1U << 14) |
If this flag is set, the transforms nfsft_trafo and nfsft_adjoint do not work. Setting this flag saves memory for precomputed data.
Definition at line 590 of file nfft3.h.
Referenced by main(), nfsft_adjoint(), nfsft_forget(), nfsft_precompute(), and nfsft_trafo().
| #define NFSFT_ZERO_F_HAT (1U << 16) |
If this flag is set, the transforms nfsft_adjoint and nfsft_direct_adjoint set all unused entries in f_hat not corresponding to spherical Fourier coefficients to zero.
Definition at line 591 of file nfft3.h.
Referenced by main(), and nfsft_adjoint().
| #define NFSFT_INDEX | ( | k, | |
| n, | |||
| plan | |||
| ) | ((2*(plan)->N+2)*((plan)->N-n+1)+(plan)->N+k+1) |
This helper macro expands to the index 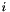 corresponding to the spherical Fourier coefficient
corresponding to the spherical Fourier coefficient 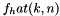 for
for 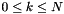 ,
, 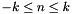 with
with
![\[ (N+2)(N-n+1)+N+k+1 \]](form_143.png)
Definition at line 594 of file nfft3.h.
Referenced by c2e(), c2e_transposed(), main(), nfsft_adjoint(), and nfsft_trafo().
| #define NFSFT_F_HAT_SIZE | ( | N | ) | ((2*N+2)*(2*N+2)) |
| #define NFSFT_DEFAULT_NFFT_CUTOFF 6 |
The default NFFT cutoff parameter.
Definition at line 62 of file nfsft.c.
Referenced by nfsft_init_advanced().
| #define NFSFT_DEFAULT_THRESHOLD 1000 |
| #define NFSFT_BREAK_EVEN 5 |
The break-even bandwidth 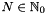 .
.
Definition at line 76 of file nfsft.c.
Referenced by nfsft_adjoint(), nfsft_forget(), nfsft_precompute(), and nfsft_trafo().
|
inline |
Compute three-term-recurrence coefficients 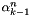 of associated Legendre functions for
of associated Legendre functions for 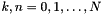 .
.
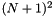 where the coefficients will be stored such that alpha[n+(N+1)+k] =
where the coefficients will be stored such that alpha[n+(N+1)+k] = 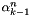 .
. 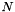 .
. Definition at line 89 of file legendre.c.
Referenced by nfsft_precompute().
|
inline |
Compute three-term-recurrence coefficients 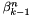 of associated Legendre functions for
of associated Legendre functions for 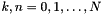 .
.
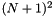 where the coefficients will be stored such that beta[n+(N+1)+k] =
where the coefficients will be stored such that beta[n+(N+1)+k] = 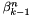 .
. 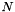 .
. Definition at line 98 of file legendre.c.
Referenced by nfsft_precompute().
|
inline |
Compute three-term-recurrence coefficients 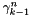 of associated Legendre functions for
of associated Legendre functions for 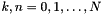 .
.
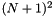 where the coefficients will be stored such that gamma[n+(N+1)+k] =
where the coefficients will be stored such that gamma[n+(N+1)+k] = 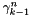 .
. 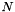 .
. Definition at line 107 of file legendre.c.
Referenced by nfsft_precompute().
| void eval_al | ( | R * | x, |
| R * | y, | ||
| const int | size, | ||
| const int | k, | ||
| R * | alpha, | ||
| R * | beta, | ||
| R * | gamma | ||
| ) |
Evaluates an associated Legendre polynomials 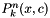 using the Clenshaw-algorithm.
using the Clenshaw-algorithm.
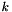
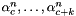
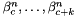
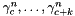
Definition at line 116 of file legendre.c.
| int eval_al_thresh | ( | R * | x, |
| R * | y, | ||
| const int | size, | ||
| const int | k, | ||
| R * | alpha, | ||
| R * | beta, | ||
| R * | gamma, | ||
| R | threshold | ||
| ) |
Evaluates an associated Legendre polynomials 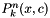 using the Clenshaw-algorithm if it no exceeds a given threshold.
using the Clenshaw-algorithm if it no exceeds a given threshold.
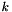
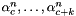
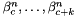
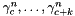
Definition at line 161 of file legendre.c.
|
inlinestatic |
Converts coefficients 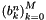 with
with 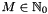 ,
, 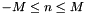 from a linear combination of Chebyshev polynomials
from a linear combination of Chebyshev polynomials
![\[ f(\cos\vartheta) = \sum_{k=0}^{2\lfloor\frac{M}{2}\rfloor} a_k (\sin\vartheta)^{n\;\mathrm{mod}\;2} T_k(\cos\vartheta) \]](form_207.png)
to coefficients 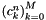 matching the representation by complex exponentials
matching the representation by complex exponentials
![\[ f(\cos\vartheta) = \sum_{k=-M}^{M} c_k \mathrm{e}^{\mathrm{i}k\vartheta} \]](form_209.png)
for each order 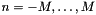 .
.
nfsft_plan containing the coefficients 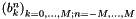
Definition at line 108 of file nfsft.c.
References nfsft_plan::f_hat_intern, nfsft_plan::N, and NFSFT_INDEX.
Referenced by nfsft_trafo(), and nfsoft_trafo().
|
inlinestatic |
Transposed version of the function c2e.
nfsft_plan containing the coefficients 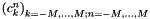
Definition at line 186 of file nfsft.c.
References nfsft_plan::f_hat, nfsft_plan::N, and NFSFT_INDEX.
Referenced by nfsft_adjoint().
| void nfsft_init | ( | nfsft_plan * | plan, |
| int | N, | ||
| int | M | ||
| ) |
Creates a transform plan.
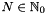
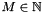
Definition at line 253 of file nfsft.c.
References nfsft_init_advanced(), NFSFT_MALLOC_F, NFSFT_MALLOC_F_HAT, and NFSFT_MALLOC_X.
| void nfsft_init_advanced | ( | nfsft_plan * | plan, |
| int | N, | ||
| int | M, | ||
| unsigned int | flags | ||
| ) |
Creates a transform plan.
nfsft_planstructure
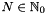
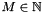
Definition at line 260 of file nfsft.c.
References FFT_OUT_OF_PLACE, FFTW_INIT, NFSFT_DEFAULT_NFFT_CUTOFF, PRE_PHI_HUT, and PRE_PSI.
Referenced by nfsft_init().
| void nfsft_precompute | ( | int | N, |
| double | kappa, | ||
| unsigned int | nfsft_flags, | ||
| unsigned int | fpt_flags | ||
| ) |
Performes precomputation up to the next power of two with respect to a given bandwidth 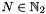 . The threshold parameter
. The threshold parameter 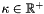 determines the number of stabilization steps computed in the discrete polynomial transform and thereby its accuracy.
determines the number of stabilization steps computed in the discrete polynomial transform and thereby its accuracy.
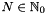
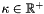
Definition at line 357 of file nfsft.c.
References nfsft_wisdom::alpha, alpha_al_all(), nfsft_wisdom::beta, beta_al_all(), FPT_AL_SYMMETRY, fpt_init(), FPT_PERSISTENT_DATA, fpt_precompute(), nfsft_wisdom::gamma, gamma_al_all(), nfsft_wisdom::initialized, nfsft_wisdom::N_MAX, nfft_free(), nfft_malloc(), NFSFT_BREAK_EVEN, NFSFT_NO_DIRECT_ALGORITHM, NFSFT_NO_FAST_ALGORITHM, nfsft_wisdom::set, nfsft_wisdom::T_MAX, and X.
Referenced by main().
| void nfsft_forget | ( | void | ) |
Forgets all precomputed data.
Definition at line 526 of file nfsft.c.
References nfsft_wisdom::alpha, nfsft_wisdom::beta, nfsft_wisdom::gamma, nfsft_wisdom::initialized, nfsft_wisdom::N_MAX, nfft_free(), NFSFT_BREAK_EVEN, NFSFT_NO_DIRECT_ALGORITHM, NFSFT_NO_FAST_ALGORITHM, and nfsft_wisdom::set.
Referenced by main().
| void nfsft_finalize | ( | nfsft_plan * | plan | ) |
Destroys a plan.
Definition at line 572 of file nfsft.c.
References nfsft_plan::f, nfsft_plan::f_hat, nfsft_plan::f_hat_intern, nfsft_plan::flags, nfft_finalize(), nfft_free(), NFSFT_MALLOC_F, NFSFT_MALLOC_F_HAT, NFSFT_MALLOC_X, NFSFT_PRESERVE_F_HAT, nfsft_plan::plan_nfft, and nfsft_plan::x.
Referenced by main().
| void nfsft_trafo | ( | nfsft_plan * | plan | ) |
Executes a NFSFT, i.e. computes for 
![\[ f(m) = \sum_{k=0}^N \sum_{n=-k}^k \hat{f}(k,n) Y_k^n\left(2\pi x_1(m), 2\pi x_2(m)\right). \]](form_135.png)
Definition at line 921 of file nfsft.c.
References c2e(), nfft_plan::f, nfsft_plan::f, nfft_plan::f_hat, nfsft_plan::f_hat, nfsft_plan::f_hat_intern, nfsft_plan::flags, nfsft_wisdom::initialized, nfsft_plan::MEASURE_TIME_t, nfsft_plan::N, nfsft_wisdom::N_MAX, nfsft_plan::N_total, nfft_elapsed_seconds(), NFSFT_BREAK_EVEN, NFSFT_INDEX, NFSFT_NO_FAST_ALGORITHM, NFSFT_NORMALIZED, NFSFT_PRESERVE_F_HAT, NFSFT_USE_DPT, NFSFT_USE_NDFT, nfsft_plan::plan_nfft, nfsft_wisdom::set, nfft_plan::x, and nfsft_plan::x.
Referenced by main().
| void nfsft_adjoint | ( | nfsft_plan * | plan | ) |
Executes an adjoint NFSFT, i.e. computes for 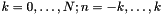
![\[ \hat{f}(k,n) = \sum_{m = 0}^{M-1} f(m) Y_k^n\left(2\pi x_1(m), 2\pi x_2(m)\right). \]](form_137.png)
Definition at line 1091 of file nfsft.c.
References c2e_transposed(), nfft_plan::f, nfsft_plan::f, nfft_plan::f_hat, nfsft_plan::f_hat, nfsft_plan::flags, fpt_transposed(), nfsft_wisdom::initialized, nfsft_plan::MEASURE_TIME_t, nfsft_plan::N, nfsft_wisdom::N_MAX, nfft_elapsed_seconds(), NFSFT_BREAK_EVEN, NFSFT_INDEX, NFSFT_NO_FAST_ALGORITHM, NFSFT_NORMALIZED, NFSFT_USE_DPT, NFSFT_USE_NDFT, NFSFT_ZERO_F_HAT, nfsft_plan::plan_nfft, nfsft_wisdom::set, nfft_plan::x, and nfsft_plan::x.
Referenced by main().
|
static |
 1.8.6
1.8.6