Next: The window function
Up: NFFT - nonequispaced fast
Previous: NFFT - nonequispaced fast
Contents
One wants to approximate the trigonometric polynomial 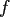 in
(2.4) by a linear combination of shifted 1-periodic window
functions
in
(2.4) by a linear combination of shifted 1-periodic window
functions
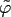 as
as
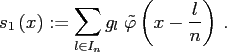 |
(2.5) |
With the help of an oversampling factor 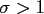 , the FFT length is given by
, the FFT length is given by
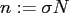 .
.
Jens Keiner
2006-11-20