NFSFT

Compared to the NFFT routines, the NFSFT module shares a similar basic procedure for computing the transformations. It differs, however, slightly in data layout and function interfaces.

The NFSFT routines depend on initially precomputed global data that limits the maximum degree N that can be used for computing transformations. This precomputation has to be performed only once at program runtime regardless of how many individual transform plans are used throughout the rest. This is done by

nfsft_precompute(N,1000,0U,0U);

Here, N is the maximum degree that can be used in all subsequent transformations, 1000 is the threshold for the FPTs used internally, and 0U and 0U are optional flags for the NFSFT and FPT. If you are unsure which values to use, leave the threshold at 1000 and the flags at 0U.

Initialisation of a plan is done by calling one of the nfsft_init-functions. We need no dimension parameter here, as in the NFFT case. The simplest version is a call to nfsft_init specifying only the bandwidth $N$ and the number of nonequispaced nodes $M$ . For an application-owned variable nfsft_plan my_plan the function call is

nfsft_init(&my_plan,N,M);

The first argument should be uninitialised. Memory allocation is completely done by the init routine.

After initialising a plan, one defines the nodes $(\vartheta_{j},\varphi_{j}) \in [0,2\pi) \times [0,\pi]$ in spherical coordinates in the member variable my_plan.x. For consistency with the other modules and the conventions used there, we use swapped and scaled spherical coordinates

$$\tilde{\varphi} := \left\{ \begin{array}{ll} \frac{\varphi}{2\pi}, & \text{if $0 ... ...rac{\varphi}{2\pi}-1, & \text{if $\pi \le \varphi < 2\pi$}, \end{array} \right. \tilde{\vartheta} := \frac{\vartheta}{2\pi}$$

and identify a point from $\mathbb{S}^2$ with the vector $(\tilde{\varphi}, \tilde{\vartheta}) \in [-\frac{1}{2}, \frac{1}{2}) \times [0,\frac{1}{2}]$ . The angles $\tilde{\varphi}_{j}$ and $\tilde{\vartheta}_{j}$ for the $j$ -th node are assigned by

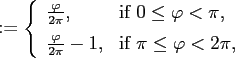my_plan.x[2*j] = /* your choice in [-0.5,0.5] */; my_plan.x[2*j+1] = /* your choice in [0,0.5] */;

After setting the nodes, the same node-dependent (see the exception above) precomputation as for the NFFT has to be performed. This is done by

nfsft_precompute_x(&my_plan);

which itself calls nfft_precompute_one_psi(&my_plan) as explained above. You might modify the precomputation strategy by passing the appropriate NFFT flags to one of the more advanced nfsft_init routines. Setting the spherical Fourier coefficients $\hat{f}_{k}^n$ in my_plan.f_hat should be done using the helper macro NFSFT_INDEX. This reads

for (k = 0; k <= N; k++)
for (n = -k; n <= k; n++)
my_plan.f_hat[NFSFT_INDEX(k,n,&plan)] = /* your choice */;

For the NFSFT, spherical Fourier coefficients are stored in a fashion different from the NFFT. You should always use the helper macro NFSFT_INDEX for setting the spherical Fourier coefficients. If, in place of a NFSFT transformation, you would like to perform an adjoint NFSFT transformation, you set the values $f\left(\vartheta_{j}, \varphi_{j}\right)$ in my_plan.f as follows:

for (j = 0; j < M; j++)
my_plan.f[j] = /* your choice */;

The actual transforms are computed by calling either nfsft_trafo(&my_plan) for the NFSFT (see Algorithm 3) or nfsft_adjoint(&my_plan) for the adjoint NFSFT (see Algorithm 4). Remember, that you must make sure that my_plan.x and my_plan.f_hat or my_plan.f have been initialised appropriately prior to calling the corresponding transformation routine. On execution, nfsft_trafo overwrites my_plan.f while nfsft_adjoint overwrites my_plan.f_hat. One only needs one plan for several transforms of the same kind, i.e. transforms with equal initialisation parameters. For comparison, the direct calculation of (3.1) and (3.5) are done by ndsft_trafo and ndsft_adjoint, respectively.

All memory allocated by the init routine is deallocated by

nfsft_finalize(&my_plan);

while the memory allocated by nfsft_precompute gets freed by calling

nfsft_forget();

Additional data, declared and allocated by the application, has to be deallocated by the user's program as well.

The library defines the structure nfsft_plan, the most important members are listed in Table 4.3. The structure contains, public read-only (r) and public read-write (w) members. The user functions for the NFSFT are collected in Table 4.4.

Table 4.3: Interesting members of nfsft_plan.

Type	Name	Size	Type	Description
int	N	1	r	Bandwidth $N$
int	N_total	1	r	Set to $4\vert\mathcal{I}_N\vert=4(N+1)^2$ ,
				quadruple of the number of Fourier coefficients
int	M_total	1	r	Total number of nodes $M$
double complex*	f_hat	$4\vert\mathcal{I}_N\vert$	w	Fourier coefficients $\hat{\mathbf{f}}$ or
				adjoint coefficients $\hat{\mathbf{h}}$
double complex*	f	$M$	w	Samples $\mathbf{f}$
double*	x	$M$	w	Sampling set $\mathcal{X}$

Table 4.4: User functions of the NFSFT.

Name	Additional arguments
nfsft_precompute	int N, double threshold,
	unsigned int nfsft_flags, unsigned int fpt_flags
nfsft_init	int N, int M
nfsft_init_advanced	int N, int M, unsigned int nfsft_flags
nfsft_init_guru	int N, int M, unsigned int nfsft_flags,
	int nfft_flags, int nfft_cutoff
nfsft_precompute_x
ndsft_trafo
ndst_adjoint
nfsft_trafo
nfsft_adjoint
nfsft_finalize
nfsft_forget

Some more things should be kept in mind when using the NFSFT module:

• The bandwidth $N_{\text{max}}$ up to which global precomputation is performed when calling nfsft_precompute is always chosen as the next power of two with respect to the specified maximum bandwidth $N$ .
• By default, the NDSFT and NFSFT transformations, ndsft_trafo and nfsft_trafo, are allowed to destroy the input f_hat while the input x is preserved. On the contrary, the adjoint NDSFT and NFSFT transformations, ndsft_adjoint and nfsft_adjoint, do not destroy the input f and x by default. The desired behaviour can be assured by using the NFSFT_PRESERVE_F_HAT, NFSFT_PRESERVE_X, NFSFT_PRESERVE_F and NFSFT_DESTROY_F_HAT, NFSFT_DESTROY_X, NFSFT_DESTROY_F flags.