



Next: Solver - inverse transforms
Up: NFSFT - nonequispaced fast
Previous: Legendre polynomials and associated
Contents
The spherical harmonics
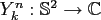 ,
,  ,
,
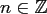 ,
are given by
,
are given by
They form an orthogonal basis for the space of square integrable functions on
the sphere, i.e.,
The orthonormal spherical harmonics are denoted by
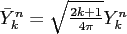 .
.
Hence, any square integrable function
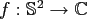 has the expansion
has the expansion
with the spherical Fourier coefficients
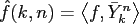 .
The function
.
The function 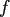 is called bandlimited, if
is called bandlimited, if
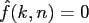 for
for 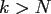 and some
and some
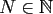 .
In analogy to the NFFT on the Torus
.
In analogy to the NFFT on the Torus
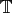 , we define the sampling set
, we define the sampling set
of nodes on the sphere 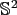 and the set of possible ''frequencies''
and the set of possible ''frequencies''
The nonequispaced discrete spherical Fourier transform (NDSFT) is
defined as the evaluation of the finite spherical Fourier sum
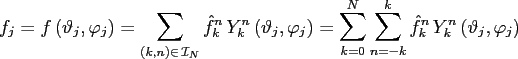 |
(3.1) |
for
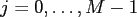 .
In matrix vector notation, this reads
.
In matrix vector notation, this reads
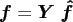 with
with
The corresponding adjoint nonequispaced
discrete fast spherical Fourier transform (adjoint NDSFT) is defined as
the evaluation of
for all
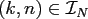 .
Again, in matrix vector notation, this reads
.
Again, in matrix vector notation, this reads
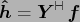 .
.
The coefficients
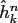 are, in general, not
identical to the Fourier coefficients
are, in general, not
identical to the Fourier coefficients
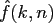 of the function
of the function 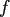 .
However, provided that for the sampling set
.
However, provided that for the sampling set
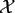 a quadrature rule
with weights
a quadrature rule
with weights 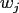 ,
,
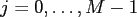 , and sufficient degree of exactness
is available, one might recover the Fourier coefficients
, and sufficient degree of exactness
is available, one might recover the Fourier coefficients
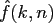 by
evaluating
by
evaluating
for all
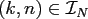 .
.
Direct algorithms for computing the NDSFT and adjoint NDSFT transformations
need
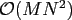 arithmetic operations.
A combination of the fast polynomial transform and the NFFT leads to
approximate algorithms with
arithmetic operations.
A combination of the fast polynomial transform and the NFFT leads to
approximate algorithms with
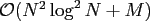 arithmetic operations.
These are denoted NFSFT and adjoint NFSFT, respectively.
The NFSFT algorithm using the FPT and the NFFT was introduced in
[34] while the adjoint NFSFT variant was developed in [32].
arithmetic operations.
These are denoted NFSFT and adjoint NFSFT, respectively.
The NFSFT algorithm using the FPT and the NFFT was introduced in
[34] while the adjoint NFSFT variant was developed in [32].
![\begin{algorithm}
% latex2html id marker 1063
[tb]
\caption[NFSFT]{Nonequispace...
...y: $\mathcal{O}\left(N^2 \log^2 N +
M\right)$.
\end{algorithmic}\end{algorithm}](img301.png)
![\begin{algorithm}
% latex2html id marker 1107
[tb]
\caption[Adjoint NFSFT]{Adjo...
...y: $\mathcal{O}\left(N^2 \log^2 N +
M\right)$.
\end{algorithmic}\end{algorithm}](img302.png)




Next: Solver - inverse transforms
Up: NFSFT - nonequispaced fast
Previous: Legendre polynomials and associated
Contents
Jens Keiner
2006-11-20
![]() has the expansion
has the expansion
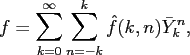
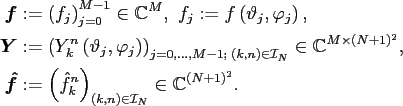
![]() are, in general, not
identical to the Fourier coefficients
are, in general, not
identical to the Fourier coefficients
![]() of the function
of the function ![]() .
However, provided that for the sampling set
.
However, provided that for the sampling set
![]() a quadrature rule
with weights
a quadrature rule
with weights ![]() ,
,
![]() , and sufficient degree of exactness
is available, one might recover the Fourier coefficients
, and sufficient degree of exactness
is available, one might recover the Fourier coefficients
![]() by
evaluating
by
evaluating
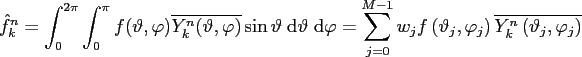
![]() arithmetic operations.
A combination of the fast polynomial transform and the NFFT leads to
approximate algorithms with
arithmetic operations.
A combination of the fast polynomial transform and the NFFT leads to
approximate algorithms with
![]() arithmetic operations.
These are denoted NFSFT and adjoint NFSFT, respectively.
The NFSFT algorithm using the FPT and the NFFT was introduced in
[34] while the adjoint NFSFT variant was developed in [32].
arithmetic operations.
These are denoted NFSFT and adjoint NFSFT, respectively.
The NFSFT algorithm using the FPT and the NFFT was introduced in
[34] while the adjoint NFSFT variant was developed in [32].