Download
Matlab Toolbox
- nhcfft-0.91.tgz
release date 2010-07, contains
HCFFT, LHCFFT and NHCFFT - nhcfft-0.9.tgz
release date 2009-06, contains
HCFFT and NHCFFT
Nonequispaced Hyperbolic Cross Fast Fourier Transform
Let a spatial dimension d ∈ ℕ and a refinement n ∈ ℕ0 be given. The hyperbolic cross Hnd and the sparse grid Snd are given by
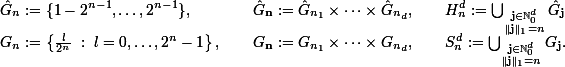 So we have |Hnd| = |Snd| ≤cd2nnd-1. We denote by Td ≅[0,1)d the d-dimensional torus, consider Fourier series ƒ: Td → ℂ and restrict the frequency domain to the hyperbolic cross.
So we have |Hnd| = |Snd| ≤cd2nnd-1. We denote by Td ≅[0,1)d the d-dimensional torus, consider Fourier series ƒ: Td → ℂ and restrict the frequency domain to the hyperbolic cross.
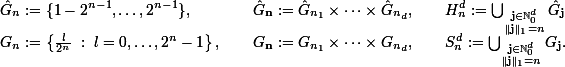
Our aim is the fast approximate evaluation of the d-variate trigonometric polynomial 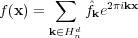 at nodes xj ∈ Td, j = 0, …, M - 1.
at nodes xj ∈ Td, j = 0, …, M - 1.
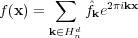 at nodes xj ∈ Td, j = 0, …, M - 1.
at nodes xj ∈ Td, j = 0, …, M - 1.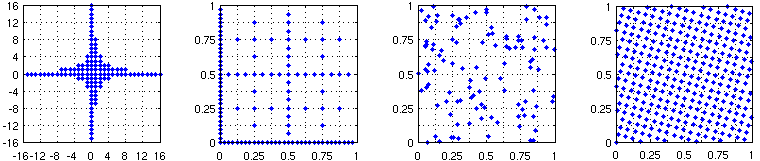
Figure 1: Hyperbolic cross, sparse grid (dimension 2, refinement 5), arbitrary sampling nodes in T2, and a nonaliasing rank-1 lattice
| Algorithm | Computational complexity |
|---|---|
| FFT with 2dn frequencies/nodes |
c2dndn |
| HCFFT | cd2nnd |
| NHCDFT | cd22nn2d-2 |
| NHCFFT | cd2nn2d-2(|log ε|d + logdn) |
| LHCFFT | c(M log M + |Hnd|) |
| Table 1: | Computational complexity of different Fourier transform algorithms |
The efficient evaluation of the trigonometric polynomial at the sparse grid nodes xj ∈ Snd, j = 0, …, |Snd| - 1, is called hyperbolic cross fast Fourier transform (HCFFT) and the reconstruction of Fourier coefficients on the hyperbolic cross from samples at the sparse grid nodes inverse HCFFT. Both transforms can be computed in cd2nnd floating point operations.
For arbitrary sampling nodes xj ∈ Td, j = 0, …, M - 1, and M = |Snd|, the naive evaluation of the trigonometric polynomial ƒ is called nonequispaced hyperbolic cross discrete Fourier transform (NHCDFT) and takes cd22nn2d-2 floating point operations. This complexity can be improved to cd2nn2d-2(|log ε|d + logdn) by means of an approximation scheme (NHCFFT) as outlined in the first manuscript below.
To evaluate a multivariate trigonometric polynomial at the nodes xj = jz / M mod 1, j = 0, …, M - 1, z ∈ ℕd, M ∈ ℕ, of a rank-1 lattice one only has to compute a one-dimensional FFT. If the rank-1 lattice allows for the exact reconstruction of the Fourier coefficients from the sample values we call it a nonaliasing lattice. This lattice based hyperbolic cross fast Fourier transform (LHCFFT) is quite simple to implement, in contrast to the HCFFT numerically stable, and takes c(M log M + |Hnd|) floating point operations. Note that the constant here is independent of d.
- Döhler, M., Kunis, S., and Potts, D.
Nonequispaced hyperbolic cross fast Fourier transform
SIAM J. Numer. Anal. 47, 4415-4428, 2010. (full paper pdf) - Kämmerer, L. and Kunis, S.
On the stability of the hyperbolic cross discrete Fourier transform
Numer. Math. 117, 581-600, 2011. (full paper pdf) - Kämmerer, L., Kunis, S., and Potts, D.
Interpolation lattices for hyperbolic cross trigonometric polynomials
J. Complexity 28, 76-92, 2012. (full paper pdf) - Kämmerer, L.
Reconstructing hyperbolic cross trigonometric polynomials by sampling along generated sets
Preprint (full paper pdf)
