Hinweis: Der Lösungsweg mit Begründung und Nebenrechnung soll deutlich erkennbar in logisch und grammatisch einwandfreien Sätzen dargestellt werden. Zur Lösungsgewinnung herangezogene Aussagen sind zu beweisen. Nur wenn eine so zu verwendende Aussage aus dem Schulunterricht oder aus Arbeitsgemeinschaften bekannt ist, genügt es ohne Beweisangabe, sie als bekannten Sachverhalt anzuführen.
390611
| (a) | Brigitte sagt:,, Ich kann die Figur A einmal so in zwei Teile zerschneiden, dass ich jede der Figuren B bis G legen kann." Zeige, dass Brigitta recht hat. |
| (b) | Einige der Figuren B bis G sind symmetrisch, andere nicht. Lege aus den beiden Teilen noch weitere drei symmetrische Figuren H, L und K ! (Wenn du die Bedeutung von "symmetrisch" nicht weißt, frage jemanden der es weiß.) |
| (c) | Bei welchen dieser Figuren B bis K musst du eines der zwei Teile umdrehen, bevor du das Zusammenbauen beginnen kannst ? |

390612
Ein Briefmarkensammler möchte auf eine Seite seines Albums ein quadratisches Muster von vier mal vier Briefmarken kleben. Er wählt dazu einen Briefmarkensatz, in dem es Marken von 1, 2, 3, 4 und 5 Groschen gibz; von allen diesen Marken hat er genügent.
Er möchte sein Mustzer so anlegen, dass folgenden Regeln gelten:
In keiner Zeile, in keiner Spalte, auf keiner Diagonalen und auf keiner Parallelen zu einer Diagonalen sollen zwei Marken mit gleichen Wert vorkommen.
| (a) | Gib eine solche Verteilung an ! |
| (b) | Der Briefmarkensammler fragt sich, welchen maximalen Wert die 16 verwendeten Briefmarken haben können. Finde diesen Wert heraus und zeige, dass sich 16 Briefmarken unter Beachtung aller Regeln so anordnen lassen (Maximaler Wert bedeutet: Es gibt keinen größeren Wert. Du musst also zeigen, dass es wirklich keinen größeren Wert gibt. |
390613
Die Zahl 32 soll als Summe von vier Zahlen dargestellt werden, die alle größer als null sind. Es soll dabei gelten: Wenn man zum ersten Summanden 3 addiert, vom zweiten Summanden 3 abzieht, den dritten Summanden mit 3 multipliziert und den vierten Summanden durch 3 teilt, so ergibt sich jedesmal dasselbe Ergebnis.
Wie lauten diese vier Zahlen ?
390614
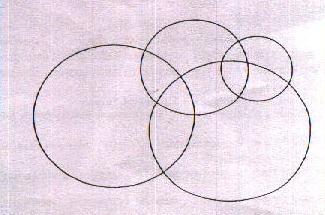
Die Abbildung 390614 zeigt ein Blatt Papier mit vier Kreisen
| (a) | Male die Abbildung 390614 vollständig mit Farben aus, befolge dabei die Regel: Keine zwei Gebiete mit einer gemeinsamen Grenzlinie sollen dieselbe Farbe bekommen. Versuche möglichst wenig Farben zu verwenden. Wie viele Farben brauchst du ? |
| (b) | Zeichne die Abbildung 390614 noch einmal ab und zeichne dann einen zusätzlichen Kreis ein, der genau einen anderen Kreis schneiden soll, und färbe wiederum nach derselben Regel! Ändert sich dadurch die Zahl der benötigten Farben ? |
| (c) | Ändert sich etwas an dieser Zahl, wenn dein zusetzlicher neuer Kreis jetzt zwei, drei, andere Kreise schneiden soll ? Kannst du dafür eine Begründung angeben ( auch wenn sie nicht verlangt wird) ? |
| (d) | Wie gehst du vor, wenn du ein Blatt, auf dem eine beliebige Anzahl von Kreisen ist, nach derselben Regel mit möglichst wenig Farben ausmalen möchtest ? Hinweis: Eine vollständige Begründung, warum bei deinem Vorgehen die gefundene Zahl der Farben ausreicht, wird nicht verlangt; dennoch wäre es schön, wenn du ein Argument angeben könntest ! |
 |