II. Klausuraufgaben:
Hinweis: Der Lösungsweg (einschließlich Nebenrechnungen) muss deutlich erkennbar sein. Alle Aussagen müssen klar formuliert und begründet werden !
4.
| Verfolgungsaufgaben gehören zu den interessanten Problemen der Mathematik. Von ihnen gibt es auch viele historische Überlieferungen. Nebenstehende Abbildung zeigt eine Aufgabe aus einem Rechenbuch von 1564, in der zwei Brüder, Heynrich und Contz, zu einer Wallfahrt nach Rom pilgern. (a) |
|
Wieviele Meilen sind es bis Rom ?
Wie viele Tage ist Contz bis Rom unterwegs ?
Nach wievielen Tagen hat Contz seinen Bruder eingeholt ?
Wie weit sind die beiden zu diesem Zeitpunkt noch von Rom entfernt
Wie weit ist Heynrich noch von Rom entfernt, wenn Contz in Rom ankommt ?
(b)
Zu einer anderen solchen Wallfahrt startet Heynrich wiederrum 9 Tage eher als Contz und legt am Tag auch 10 Meilen zurück. Contz möchte seinen Bruder nach 30 Tagen einholen, muss aber auf dem ersten Stück einen Umweg von 45 Meilen gehen.
Berechne, wie viele Meilen Contz nun täglich zurücklegen muss !
5.
Wir betrachten quadratische Spielfelder aus n (waagerechten) Zeilen und n (senkrechten) Spalten. Sie bestehen also aus n x n Feldern.
Auf ein solches Spielfeld soll eine bestimmte Anzahl von Türmen so aufgestellt werden, dass sie einnander nicht bedrohen. Ein Turm bedroht genau diejenigen Felder, die in der Zeile oder der Spalte liegen, in der der Turm steht (siehe Abb.1).
Zwei Anordnungen von Türmen auf einem Spielfeld gelten genau dann als gleich, wenn sie durch Drehungen oder Spiegelungen auseinander hervorgegangen sind.
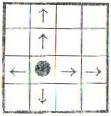
Abb.1
| (a) | Auf einem 3x3-Spielfeld gibt es genau zwei verschiedene Anordnungen von 3 Türmen, bei der dieser einander nicht bedrohen.
Zeichne diese beiden Anordnungen ! Zeichne zu jeder dieser Anordnungen alle diejenigen Anordnungen, die durch Spiegelungen oder Drehungen aus ihr hervorgehen und nicht mit ihr identisch sind ! |
| (b) | Zeichne alle verschiedene Anordnung, die 4 Türme auf einem 4x4-Spielfeld einnehmen können, ohne dabei einnander zu bedrohen ! Wie viele verschiedene derartige Anordnung gibt es ? |
| (c) | Gegeben sei ein 4x4-Spielfeld, in dessen Felder Zahlen von 1 bis 16 so eingetragen sind, wie in Abb.2 angegeben. Wir betrachten alle in Teil b) gefundenen Anordnungen von 4 Türmen, die einander nich bedrohen, und bilden jeweils die Summe der Felder, auf denen diese Türme stehen. Erstaunlicherweise sind alle diese Summen gleich ! Gib diese gemeinsame Summe an ! |
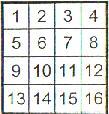
Abb. 2
