



Next: Legendre polynomials and associated
Up: NFSFT - nonequispaced fast
Previous: NFSFT - nonequispaced fast
Contents
Every point in
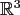 can be described in spherical coordinates by a vector
can be described in spherical coordinates by a vector
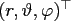 with the radius
with the radius 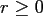 and two angles
and two angles
![$ \vartheta \in [0,\pi ]$](img11.png) ,
,
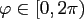 .
We denote by
.
We denote by 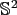 the two-dimensional unit sphere embedded into
the two-dimensional unit sphere embedded into
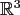 ,
i.e.
,
i.e.
and identify a point from 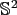 with the corresponding vector
with the corresponding vector
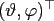 .
The spherical coordinate system is illustrated in Figure 3.2.
.
The spherical coordinate system is illustrated in Figure 3.2.
Figure:
The spherical coordinate system in
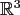 : Every point
: Every point
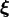 on a
sphere with radius
on a
sphere with radius  centred at the origin can be described by angles
centred at the origin can be described by angles
![$ \vartheta \in [0,\pi ]$](img11.png) ,
,
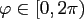 and the radius
and the radius
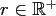 .
For
.
For
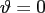 or
or
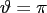 the point
the point
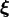 coincides with the
North or the South pole, respectively.
coincides with the
North or the South pole, respectively.
|
|
Jens Keiner
2006-11-20
![\includegraphics[width=0.60\textwidth]{images/sphere}](img256.png)