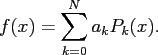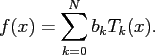Next: NFSFT - nonequispaced fast
Up: Generalisations and inversion
Previous: NSFFT - nonequispaced sparse
Contents
FPT - fast polynomial transform
A discrete polynomial transform (DPT) is a generalisation of the DFT
from the basis of complex exponentials
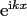 to an
arbitrary systems of algebraic polynomials satisfying a three-term recurrence
relation.
More precisely, let
to an
arbitrary systems of algebraic polynomials satisfying a three-term recurrence
relation.
More precisely, let
![$ P_{0},P_{1},\hdots:[-1,1]\rightarrow\ensuremath{\mathbb{R}}$](img231.png) be a sequence of
polynomials that satisfies a three-term recurrence relation
be a sequence of
polynomials that satisfies a three-term recurrence relation
with
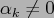 ,
, 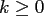 ,
,
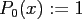 , and
, and
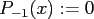 .
Clearly, every
.
Clearly, every 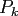 is a polynomial of exact degree
is a polynomial of exact degree 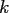 and typical
examples are the classical orthogonal Jacobi polynomials
and typical
examples are the classical orthogonal Jacobi polynomials
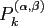 .
.
Now, let
![$ f:[-1,1]\rightarrow\ensuremath{\mathbb{R}}$](img240.png) be a polynomial of degree
be a polynomial of degree
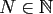 given by
the finite linear combination
given by
the finite linear combination
The discrete polynomial transform (DPT) and its fast version, the fast
polynomial transform (FPT), are the transformation of the coefficients
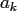 into coefficients
into coefficients 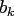 from the orthogonal expansion of
from the orthogonal expansion of 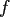 into
the basis of Chebyshev polynomials of the first kind
into
the basis of Chebyshev polynomials of the first kind
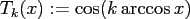 , i.e.,
, i.e.,
A direct algorithm for computing this transformation needs
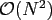 arithmetic operations.
The FPT algorithm implemented in the NFFT library follows the approach in
[51] and is based on the idea of using the three-term-recurrence
relation repeatedly.
Together with a method for fast polynomial multiplication in the Chebyshev
basis and a cascade-like summation process, this yields a method for computing
the polynomial transform with
arithmetic operations.
The FPT algorithm implemented in the NFFT library follows the approach in
[51] and is based on the idea of using the three-term-recurrence
relation repeatedly.
Together with a method for fast polynomial multiplication in the Chebyshev
basis and a cascade-like summation process, this yields a method for computing
the polynomial transform with
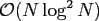 arithmetic operations.
For more detailed information, we refer the reader to
[12,13,51,44,32] and the references therein.
arithmetic operations.
For more detailed information, we refer the reader to
[12,13,51,44,32] and the references therein.




Next: NFSFT - nonequispaced fast
Up: Generalisations and inversion
Previous: NSFFT - nonequispaced sparse
Contents
Jens Keiner
2006-11-20
![]() be a polynomial of degree
be a polynomial of degree
![]() given by
the finite linear combination
given by
the finite linear combination