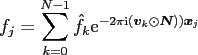NNFFT - nonequispaced in time and frequency fast Fourier transform

Now we are interested in the computation of

$$f_j= \sum_{k=0}^{N-1} \hat f_k {\rm e}^{-2\pi{\mbox{\scriptsize {... ...ol{v}}_k\odot \ensuremath{\boldsymbol{N}}\right))\ensuremath{\boldsymbol{x}}_j}$$

for $j=0,\hdots,M-1$ , $\ensuremath{\boldsymbol{v}}_k, \ensuremath{\boldsymbol{x}}_j \in \ensuremath{\mathbb{T}}^d$ , and $\hat f_k \in \ensuremath{\mathbb{C}}$ , where $\ensuremath{\boldsymbol{N}}\in \ensuremath{\mathbb{N}}^d$ denotes the "nonharmonic" bandwidth. The corresponding fast algorithm is known as fast Fourier transform for nonequispaced data in space and frequency domain (NNFFT) [15,18,52] or as type 3 nonuniform FFT [38].

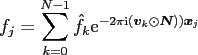A straightforward evaluation of this sum with the standard NFFT is not possible, since the samples in neither domain are equispaced. However, an so-called NNFFT was first suggested in [15] and later studied in more depth in [18], which permits the fast calculation of the Fourier transform of a vector of nonequispaced samples at a vector of nonequispaced positions. It constitutes a combination of the standard NFFT and its adjoint see also [52].