-Achse, so dass die Projektion von
auf die
-Ebene in die
-Achse gedreht wird.
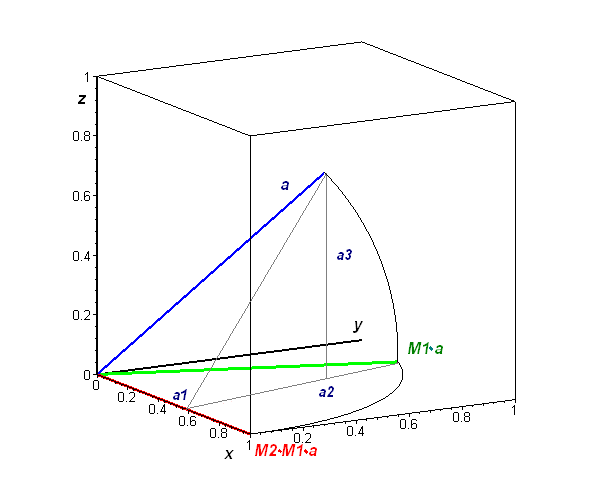
Herleitung der Drehung um eine Achse a im Raum durch Drehungen um Koordinatenachsen.
| > | with(linalg): a:=vector(3,[]): |
Drehung um die
-Achse, so dass die Projektion von
auf die
-Ebene in die
-Achse gedreht wird.
| > | c1:=a[2]/sqrt(a[2]^2+a[3]^2): s1:=a[3]/sqrt(a[2]^2+a[3]^2): M1:=matrix(3,3,[1,0,0,0,c1,s1,0,-s1,c1]); |
![M1 := matrix([[1, 0, 0], [0, a[2]/(a[2]^2+a[3]^2)^(1/2), a[3]/(a[2]^2+a[3]^2)^(1/2)], [0, -a[3]/(a[2]^2+a[3]^2)^(1/2), a[2]/(a[2]^2+a[3]^2)^(1/2)]])](images/Drehung_um_a6.gif)
Dann liegt das Bild von
in der
-Ebene:
| > | a2:=map(simplify,multiply(M1,a)); |
![a2 := vector([a[1], (a[2]^2+a[3]^2)^(1/2), 0])](images/Drehung_um_a9.gif){kind=small}
Nun drehen wir um die
-Achse, so dass das Bild von
nun wiederum auf die
-Achse abgebildet wird:
| > | c2:=subs(a[1]^2=1-a[2]^2-a[3]^2,simplify(a2[1]/sqrt(a2[1]^2+a2[2]^2))); s2:=subs(a[1]^2=1-a[2]^2-a[3]^2,simplify(a2[2]/sqrt(a2[1]^2+a2[2]^2))); |
![c2 := a[1]](images/Drehung_um_a13.gif){kind=small}
![s2 := (a[2]^2+a[3]^2)^(1/2)](images/Drehung_um_a14.gif){kind=small}
| > | M2:=matrix(3,3,[c2,s2,0,-s2,c2,0,0,0,1]); |
![M2 := matrix([[a[1], (a[2]^2+a[3]^2)^(1/2), 0], [-(a[2]^2+a[3]^2)^(1/2), a[1], 0], [0, 0, 1]])](images/Drehung_um_a15.gif)
Probe:
![a[3] = M[2]*M[1]*a](images/Drehung_um_a16.gif){kind=small}
| > | a3:=multiply(M2,a2); subs(a[1]^2=1-a[2]^2-a[3]^2,evalm(map(simplify,a3))); |
![a3 := vector([a[1]^2+a[2]^2+a[3]^2, 0, 0])](images/Drehung_um_a17.gif){kind=small}
![vector([1, 0, 0])](images/Drehung_um_a18.gif){kind=small}
Jetzt die eigentliche Drehung um diese Achse um einen Winkel
M3:=matrix(3,3,[1,0,0,0,cos(phi),-sin(phi),0,sin(phi),cos(phi)]);
![M3 := matrix([[1, 0, 0], [0, cos(phi), -sin(phi)], [0, sin(phi), cos(phi)]])](images/Drehung_um_a20.gif)
Die Gesamtdrehung
![M[1]^T*M[2]^T*M[3]*M[2]*M[1]](images/Drehung_um_a21.gif){kind=small}
kann Maple nicht ohne Hilfe auf die gew�nschte Form bringen ...
| > | MM:=map(simplify,subs(a[2]^2+a[3]^2=1-a[1]^2,multiply(transpose(M1),transpose(M2),M3,M2,M1))); |
![MM := matrix([[a[1]^2+cos(phi)-a[1]^2*cos(phi), a[2]*a[1]-a[2]*a[1]*cos(phi)-sin(phi)*a[3], a[3]*a[1]-a[3]*a[1]*cos(phi)+sin(phi)*a[2]], [a[2]*a[1]-a[2]*a[1]*cos(phi)+sin(phi)*a[3], -(a[2]^2-a[2]^2*a[1...](images/Drehung_um_a22.gif)
| > | # a[1]^2+(1-a[1]^2)*cos(phi)=cos(phi)+a[1]^2*(1-cos(phi)); |
| > | for i from 2 to 3 do for j from 2 to 3 do MM[i,j]:=simplify(subs(a[1]^2=(1-a[2]^2-a[3]^2),MM[i,j])); od: od: print(MM); |
![matrix([[a[1]^2+cos(phi)-a[1]^2*cos(phi), a[2]*a[1]-a[2]*a[1]*cos(phi)-sin(phi)*a[3], a[3]*a[1]-a[3]*a[1]*cos(phi)+sin(phi)*a[2]], [a[2]*a[1]-a[2]*a[1]*cos(phi)+sin(phi)*a[3], a[2]^2-cos(phi)*a[2]^2+co...](images/Drehung_um_a23.gif)
usw.
