Einleitung
Synthesizer sind elektronische Musikinstrumente, die durch unterschiedliche Formen der Klangsynthese Töne erzeugen. Aus musikalischer Sicht gehören sie damit zu den Elektrophonen (deutsch etwa ‚Elektroklinger‘). Seit dem Erscheinen erster kommerzieller Geräte Mitte der 1960er Jahre sind Synthesizer ein fester und mitunter stilprägender Bestandteil der Rock- und Pop-Musik.
Für die Klangsynthese existiert eine Vielzahl von Mechanismen. Sie alle haben zum Ziel, Schwingungen mit Frequenzen im hörbaren Bereich zu erzeugen und zu beeinflussen. Damit bieten Synthesizer – neben ihrer musikalischen Bedeutung – auch ein Umfeld zur physikalischen Untersuchung einfacher und komplexer Schwingungsvorgänge.
Während die Synthesizer der ersten Generation noch die Größe eines Kleiderschranks besaßen, existieren heute neben kompakten analogen und digitalen Geräten auch reine Software-Synthesizer, die auf Standard-PCs und Tablets laufen. Die (zum Teil kostenfreie) Verfügbarkeit solcher Systeme stellt ein weiteres Argument für die Nutzung von Synthesizern zur Untersuchung von Schwingungen dar.
An dieser Stelle setzt der vorliegende Bericht an. Anhand eines Software-Synthesizers werden einfache und komplexere Schwingungsverläufe erzeugt und modifiziert. Neben der physikalischen Beschreibung der jeweiligen Schwingungen soll auch der sich daraus ergebende Höreindruck charakterisiert werden. Details der menschlichen Hörwahrnehmung liegen dabei jedoch außerhalb des Rahmens dieses Berichts.
Grundlagen
Schwingungen und Klänge
In der Physik bezeichnet der Begriff Schwingung die zeitlich periodische Änderung einer beliebigen physikalischen Größe. Im einfachsten Fall wird eine Schwingung durch eine Sinus- oder Kosinusfunktion beschrieben. Für eine allgemeine Größe \(a\) könnte diese lauten:
\[a(t) = a_\mathrm{max} \cdot \sin (2\pi f \cdot t + \varphi_0) \, .\]
Dabei bezeichnet \(a_\mathrm{max}\) die Amplitude, \(f\) die Frequenz und \(\varphi_0\) die Anfangsphase der Schwingung. Eine Schwingung, die – wie in der obigen Gleichung – durch eine einzelne Sinus- (oder Kosinus-) Funktion beschrieben wird, wird als harmonisch bezeichnet.
In der Akustik wird ein Schallereignis, das aus einer einzigen harmonischen Schwingung besteht, als Ton bezeichnet. Leider werden die Begriffe ›Ton‹ und ›Klang‹ in Akustik und Musik unterschiedlich verwendet. In der Musik besteht ein Ton aus mehreren harmonischen Schwingungen. Die Frequenzen dieser Harmonischen sind dabei allesamt ganzzahlige Vielfache der Grundfrequenz, also der niedrigsten vorhandenen Frequenz. In der Akustik entspricht dies dem Begriff Klang. Musikalisch wiederum entsteht ein Klang aus der Mischung mehrerer Töne. Die auftretenden Frequenzen lassen sich dann nicht mehr als Vielfache einer einzelnen Frequenz angeben.
Entscheidend für einen Ton in der Musik ist, dass ihm eine Tonhöhe zugeordnet werden kann. Die wahrgenommene Tonhöhe wird bestimmt durch die Frequenz der Schwingung, die diesen Ton erzeugt. Bei mehreren vorhanden Frequenzen (wie es für einen musikalischen Ton charakteristisch ist), bestimmt in der Regel die Grundfrequenz, also die niedrigste vorhandene Frequenz die Tonhöhe. Große Frequenzen erzeugen dabei hohe Töne, während niedrige Frequenzen zu tiefen Tönen führen. Der als Referenz für das Stimmen von Instrumenten häufig genutzte „Kammerton“ A (musikalisch: eingestrichenes A, \(a'\)) hat beispielsweise eine Frequenz von \(f_\mathrm A = 440~\mathrm{Hz}\).
Die vorliegende Arbeit folgt keiner der oben aufgeführten Begriffsdefinitionen streng, sondern orientiert sich an der allgemeinsprachlichen Verwendung der Wörter Ton und Klang. Eine derart scharfe Abgrenzung zwischen den Begrifflichgkeiten wie oben angegeben liegt bei dieser Verwendung nicht vor.
Ein Klang, der durch die Überlagerung mehrerer harmonischer Schwingungen ensteht, stellt einen komplexen Schwingungsvorgang dar. Zudem ändert sich diese Schwingung im Verlauf der Zeit vom Anklingen über ein (mehr oder minder) konstantes Aushalten des Klangs bis zum Abklingen. Zur Erzeugung derartiger Vorgänge, ebenso wie zu deren Charakterisierung, braucht es geeignete Werkzeuge. Für die Klangsynthese existiert eine Vielzahl unterschiedlicher Herangehensweisen, von denen das Prinzip der subtraktiven Synthese für diesen Bericht vorwiegend genutzt wird. Für die Charakterisierung von Klängen dient zunächst die grafische Darstellung des zeitlichen Schwingungsverlaufs in einem \(a(t)\)-Diagramm (wobei \(a\) allgemein für eine Größe steht, die die akustische Schwingung charakterisiert). Daneben (und mindestens gleichwertig) wird die Analyse der in einer komplexen Schwingung auftretenden Frequenzen mittels Fouriertransformation genutzt.
Fourier-Transformation
Wie oben bereits erwähnt, besteht ein Klang aus mehreren Schwingungen unterschiedlicher Frequenz. Die Analyse der Frequenzzusammensetzung einer komplexen Schwingung beruht auf dem Fourier-Theorem. Dieses besagt, dass jeder periodische Vorgang (oder mathematisch ausgedrückt: jede periodische Funktion) als Summe von Harmonischen ausgedrückt werden kann. Mathematisch erfolgt der Übergang von einer zeitabhängigen Funktion \(a(t)\) zu deren Frequenzspektrum \(A(f)\) durch die Fouriertransformation:
\[A(f) = \mathcal F\big(a(t)\big) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} a(t) e^{-i2\pi ft} \mathrm dt \, .\]
Mathematisch betrachtet liefert die Fouriertransformation auch Amplitudenwerte für negative Frequenzen. Im Sinne der Akustik sind jedoch nur Frequenzen \(f>0\) – also der positive Definitionsbereich von \(\mathcal F\big(a(t)\big)\) – relevant, und nur diese werden im weiteren Verlauf dieses Berichts betrachtet.
Ist die Funktion \(a(t)\) eine harmonische Schwingung der Frequenz \(f_0\), so zeigt die Fouriertransformierte (im positiven Bereich) einen scharfen Peak bei ebendieser Frequenz \(f_0\). Für komplexe Schwingungsvorgänge enthält die Fouriertransformierte mehrere Peaks als Intensitätsverteilung aller auftretenden Frequenzen.
Es sei angemerkt, dass die Fouriertransformation nicht auf periodische Funktionen beschränkt ist. Das oben angegebene Fourierintegral lässt sich auf beliebige Funktionen anwenden. Die Fouriertransformation enthält dann keine scharfen Peaks sondern eine breitere Intensitätsverteilung.
Umgekehrt zur obigen Vorgehensweise lässt sich aus einem Frequenzspektrum \(A(f)\) die resultierende Schwingung \(a(t)\) durch inverse Fouriertransformation ermitteln:
\[a(t) = \mathcal F^{-1}\big(A(f)\big) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} A(f) e^{i2\pi ft} \mathrm df \, .\]
Der in beiden Gleichungen auftretende Vorfaktor \(\frac{1}{\sqrt{2\pi}}\) normiert die Absolutwerte bei der Transformation, sodass gilt
\[a(t) = \mathcal F^{-1}\Big(\mathcal F\big(a(t)\big)\Big) \, .\]
Ohne die Normierungsfaktoren hätte das Ergebnis nach Hin- und Rücktransformation andere Absolutwerte als die Ausgangsfunktion.
Die oben angegebene Gleichung der Fouriertransformation bezieht sich auf eine als Funktionsgleichung gegebene Funktion \(a(t)\). Werden hingegen Kurvenverläufe digital aufgezeichnet (wie auch in diesem Bericht), so bestehen diese aus einer großen Anzahl diskreter Wertepaare der Form \(\big(t, a(t)\big)\). Die Bestimmung des Frequenzspektrums einer solchen Funktion geschieht dann durch diskrete Fouriertransformation (DFT). Der Wesentliche Unterschied zu den obigen Gleichungen ist dabei, dass das Integral ersetzt wird durch eine Summe über alle Wertepaare. Anstelle der Bezeichnung DFT wird häufig die Abkürzung FFT verwendet. Diese steht für ‚Fast Fourier Transform‘ und bezeichnet einen Algorithmus der diskreten Fouriertransformation, der sich rechentechnisch besonders schnell lösen lässt.
An dieser Stelle sei noch auf zwei Eigenschaften eines durch diskrete Fouriertransformation erzeugten Frequenzspektrums hingewiesen:
- Die größte erfassbare Frequenz wird durch die zeitliche Auflösung der \(a(t)\)-Kurve bestimmt. Je besser diese Auflösung (höhere Abtastrate), umso größere Frequenzen können erfasst werden. Die Abtastrate bestimmt also die hochfrequente Grenze der DFT, wobei die maximale Frequenz nicht höher als die Hälfte der Abtastrate sein kann 1.
- Die kleinste erfassbare Frequenz und somit die Frequenzauflösung wird bestimmt durch die zeitliche Dauer des \(a(t)\)-Signals. Je größer diese Dauer ist, umso kleinere Frequenzen können erfasst werden und umso feiner wird die Auflösung des Frequenzspektrums.
Methoden der Klangsynthese
Für die Erzeugung eines Klangs haben sich verschiedene Herangehensweisen etabliert. Alle diese Formen der Klangsynthese erzeugen ein jeweils charakteristisches Klangbild und weisen für den musikalischen Einsatz spezifische Vor- und Nachteile auf.
Aus physikalischer Sicht mag es naheliegend erscheinen, einen gewünschte Klang als Fourier-Synthese durch Kombination einer (mehr oder minder großen) Anzahl harmonischer Schwingungen zusammen zu setzen. Tatsächlich wird dieses Prinzip der additiven Synthese auch in einigen Synthesizern angewendet. Ihre Realisierung wurde aber erst durch digitale Geräte praktisch möglich. Die ersten Synthesizer arbeiteten mit rein analoger Elektronik. Für jede Harmonische würde hier ein eigener Schwingkreis benötigt, die allesamt zueinander (und in einer Band auch zu anderen Instrumenten) in Stimmung gehalten werden müssten. Angesichts von unvermeidbaren Instabilitäten der einzelnen Schwingkreise (unter anderem bedingt durch Temperaturabhängigkeit der einzelnen Bauelemente) war dies für mehrere zehn Schwingkreise, wie sie für die additive Synthese eines Klangs erforderlich wären, praktisch nicht realisierbar. Ein Vor- und Nachteil gleichermaßen der additiven Synthese ist die Vielzahl der einzustellenden Parameter, da für jede Harmonische einzeln Lautstärke und zeitlicher Verlauf einzustellen sind. Das erlaubt sehr viele Freiheitsgrade bei der Gestaltung eines Klangs, erfordert aber gleichzeitig auch einen entsprechend hohen Aufwand bei der Einstellung dieser Parameter.
Neben Synthesizern die vollständig oder überwiegend auf der additiven Synthese beruhen, besitzen auch andere Typen häufig eine additive Komponente, da die Schwingungen verschiedener Oszillatoren überlagert werden.
Die ersten kommerziellen Synthesizer nutzten das Prinzip der subtraktiven Synthese, was bis heute vielleicht so etwas wie der ‚klassische‘ Synthesizer ist. Hierbei wird von einem Oszillator eine obertonreiche Schwingung wie Rechteck- oder Sägezahnschwingung erzeugt. Durch nachgeschaltete Filter wird dann das Obertonspektrum dieser Schwingung modifiziert, indem bestimmte Frequenzanteile gedämpft werden – daher auch die Bezeichnung subtraktive Synthese. Auch der für diesen Bericht eingesetzte Software-Synthesizer nutzt hauptsächlich das Prinzip der subtraktiven Synthese. Die typischen Elemente eines solchen Geräts (beziehunsgweise einer solchen Software) werden im Laufe dieses Berichts anhand ihres jeweiligen Einsatzes vorgestellt und sollen hier nicht vorweggenommen werden.
Neben den oben beschriebenen Typen der Klangsynthese existiert eine Vielzahl weiterer Syntheseformen. Dazu gehören unter anderem die Frequenzmodulations- (FM) Synthese, die Wavetable-Synthese oder das Physical Modelling. Eine tiefergehende Beschreibung aller dieser Syntheseformen liegt jedoch außerhalb des Rahmens dieses Berichts. Eine praxisorientierte Einführung in die verschiedenen Syntheseformen ist beispielsweise in 2 zu finden.
Experimentelle Details
Verwendete Geräte & Software
Für diesen Bericht wurde der Software-Synthesizer AudioKit Synth One verwendet, der für iPad und iPhone verfügbar ist. In seinen Grundfuktionen bildet diese Software einen klassischen substraktiven Synthesizer nach, bietet aber darüber hinaus Möglichkeiten, die über die eines klassischen Geräts hinausgehen. Ein Überblick über die Funktionen des SynthOne ist in 3 zu finden. Auf die einzelnen Features dieser App soll im Verlaufe dieses Berichts bei ihrer jeweiligen Anwendung eingegangen werden.
Hardwareseitig kommt ein Apple iPad Pro (12,9 Zoll) zum Einsatz, auf dem die Synth One App betrieben wird. Die Ausgabe der erzeugten Klänge erfolgt über die Kopfhörerbuchse. Zur Pegeleinstellung und Signalverteilung wird ein kleines Audio-Mischpult (Behringer XENYX Q802USB) benutzt. Da dieses die erzeugten Klänge unbeeinflusst lassen soll, wurden alle Klangregler in eine neutrale Position gebracht. Zur Klangbeurteilung wurden einfache In-Ear-Kopfhörer oder Lautspreche verwendet, die an den Kopfhörerausgang beziehundsweise den Monitorausgang des Mischpults angeschlossen wurden. Die Aufzeichnung der Schwingungsverläufe erfolte mit einem USB-Oszilloskop (PicoScope 2205A), das an den Ausgang (Main Out) des Mischpults angeschlossen war. Anzumerken ist, dass hierbei nur der linke Kanal genutzt wurde. Stereo-Effekte des Synthesizers lassen sich damit nicht abbilden und blieben in diesem Bericht unberücksichtigt. Aufnahme der Schwingungsverläufe und Berechnung von Frequenzspektren via FFT erfolgten in der Software PicoScope 7.
Zum Spielen des Synthesizers besitzt Synth One eine virtuelle Klaviertastatur, die direkt auf dem Display gespielt wird. Aufgrund der besseren Handhabung wurde dies ergänzt durch ein MIDI-Masterkeyboard (Nektar SE 49), das via USB mit dem iPad verbunden war.
Vorgehensweise
Der Funktionsumfang von Synth One bietet einen weiten Gestaltungsspielraum für die Erzeugung von Klängen. Der Schwerpunkt dieses Berichts liegt jedoch nicht auf einer möglichst komplexen Klangsynthese, sondern auf der physikalischen Sichtweise auf die Erzeugung und Modifierung von (akustischen) Schwingungen. In diesem Sinne beginnen die Untersuchungen mit den grundlegenden Schwingungsformen und arbeiten sich danach durch verschiedene Aspekte der Klangbeeinflussung. Zur quantitativen Beurteilung der Klänge werden sowohl die Darstellung des zeitlichen Schwingungsverlaufs als auch das zugehörige Frequenzspektrum genutzt. Ergänzt wird dies an einigen Stellen durch die Beschreibung des Klangeindrucks der durch die jeweilige Schwingung hervorgerufen wird. Letzteres ist selbstverständlich eine subjektive Angelegenheit und erhebt nicht den Anpruch einer umfassenden Klangbeurteilung.
Messgrößen
Am Oszilloskop werden grundsätzlich Spannungen gemessen. Dementsprechend erfolgen Amplitudenangaben als Spannungswerte. Absolutwerte der Amplituden besitzen dabei keine Aussagekraft, da sie von der Einstellung des Tablets (Lautstärke am Kopfhörerausgang) und des Mischpults abhängig sind. Relevant sind Amplitudenverhältnisse unterschiedlicher Oberschwingungen.
Da sich die Amplitudenwerte der in einem Klang enthaltenen Schwingungen oftmals über mehrere Größenordnungen erstrecken, erfolgt insbesondere in den Frequenzspektren eine Angabe des Spannungspegels \(L_\mathrm V\) in der Einheit Dezibel. Dieser Pegel ist für eine Spannung \(U\) definiert als:
\[L_\mathrm V = 10\lg\frac{U^2}{U_0^2} = 20\lg\frac{U}{U_0} \, ,\]
wobei als Bezugswert \(U_0 = 1~\mathrm V\) gilt. Für das Verhältnis zweier Spannungswerte \(U_1\) und \(U_2\), die als Spannungspegel \(L_\mathrm{V,1}\) und \(L_\mathrm{V,2}\) gegeben sind, folgt daraus:
\[\frac{U_2}{U_1} = 10^\frac{L_\mathrm{V,2} - L_\mathrm{V,1}}{20} \, .\]
Auf diese Weise lassen sich Amplitudenverhältnisse direkt aus den jeweiligen Pegeln ermitteln. Eine Umrechnung der Einzelpegel in Spannungswerte ist nicht erforderlich.
Messungen, Ergebnisse und Diskussion
Grundlegende Schwingungsformen
Ausgangspunkt für die Klangsynthese ist die Erzeugung einer (oderm mehrerer) Schwingung(en). Subtraktive Synthesizer bieten hierfür in der Regel verschiedene Schwingungsformen an.
Für die Untersuchungen in diesem Abschnitt werden nur die jeweiligen Schwingungserzeuger genutzt. Alle anderen Elemente der Klangbeeinflussung werden auf ein möglichst neutrales Verhalten eingestellt. Konkret bedeutet das:
- Der Filter ist auf Low Pass eingestellt, wobei die Cutoff-Frequenz auf den maximalen Wert gestellt ist. Die Resonanz des Filters ist auf ihr Minimum gestellt.
- Für die Amplitude Envelope sind alle Zeiten (Attack, Decay, Release) auf Null gestellt. Für das Sustain sind \(100~\%\) eingestellt.
Sinusschwingung
Die grundlegendste Schwingungsform ist eine reine Sinusschwingung. In der verwendeten Synthesizer-App ist diese Schwingungsform ein wenig versteckt, da sie sich nicht bei den beiden Oszillatoren (Abschnitte OSC 1 & OSC 2 im Tab MAIN) befindet. Stattdessen findet sich die Sinusschwingung als Trägerfrequenz des FM-Synthesizers (Abschnitt FM im Tab MAIN). Um eine reine Sinusschwingung auszugeben muss daher der Volume-Regler im FM-Abschnitt auf einen endlichen Wert eingestellt werden, während alle anderen Klangerzeuger (OSC 1, OSC 2, Sub und Noise) auf Null eingestellt werden.
Mit diesen Einstellungen wurde der Ton \(a'\) („Kammerton“) mit \(f_{a'} = 440~\mathrm{Hz}\) gespielt und aufgezeichnet. Das Oszillogramm (siehe nachstehende Abbildung) zeigt eine Sinuskurve als zeitlichen Verlauf der Schwingung. Da es sich hierbei um eine einzelne harmonische Schwingung handelt, zeigt das zugehörige Frequenzspektrum einen einzelnen scharfen Peak bei der Frequenz des Tons.
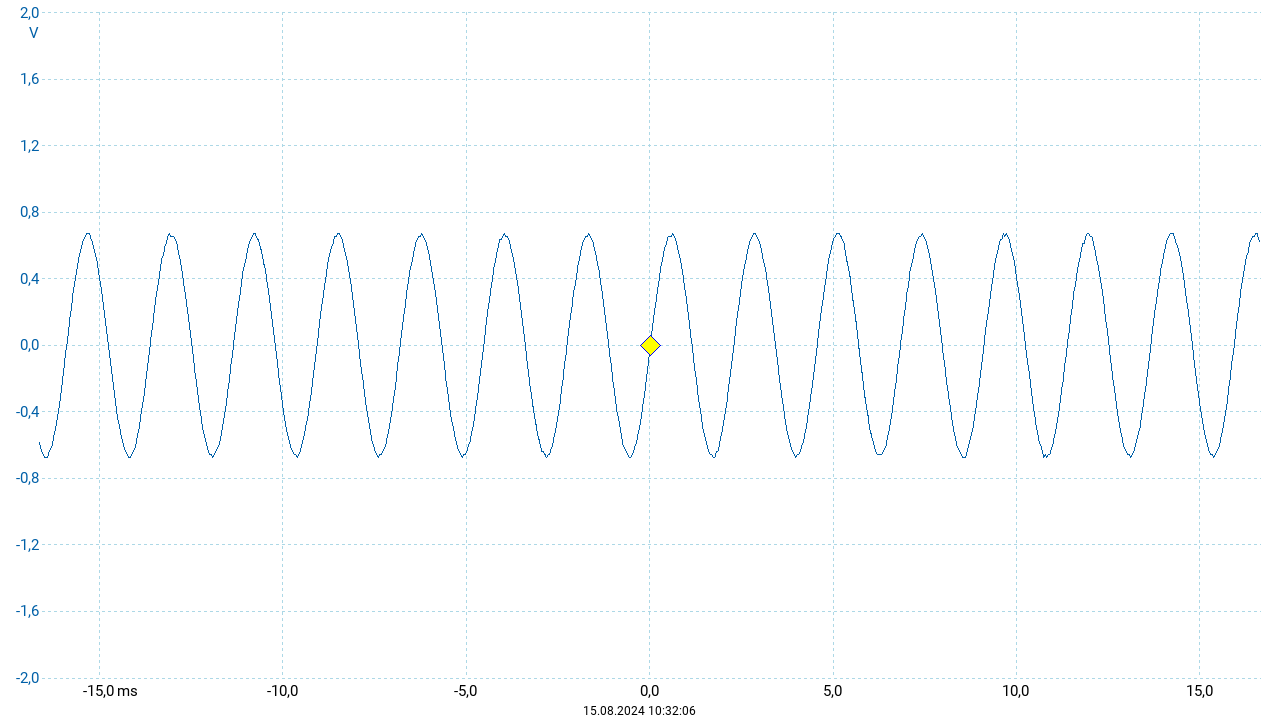
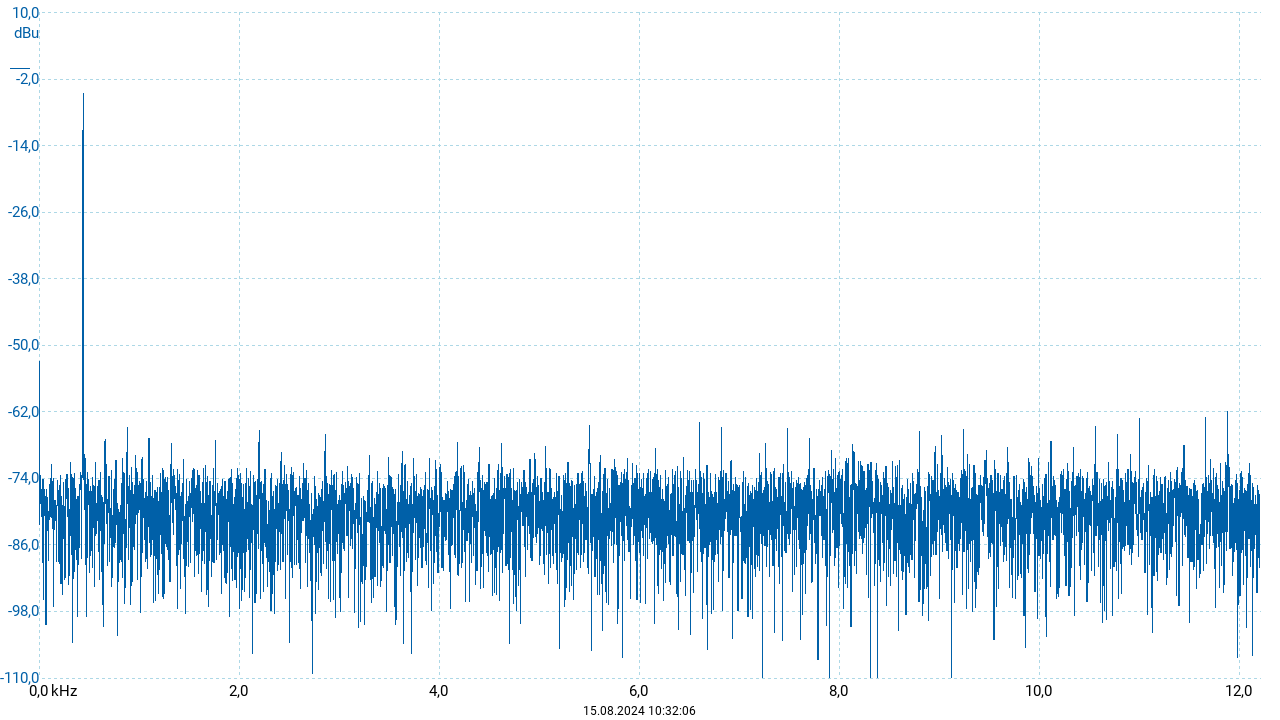
In der Wahrnehmung erscheint ein solcher Sinuston zunächst als eher weich und dumpf. Der Ton weist im zeitlichen Verlauf keinerlei Veränderungen auf. Daher wird er bereits nach wenigen Sekunden, in denen er unverändert klingt, als störend empfunden.
Dreieckschwingung
Die Synthesizer-App bietet die Dreieckschwingung doppelt an (OSC 1 und OSC 2). An dieser Stelle wird nur OSC 1 verwendet, für den die Wellenform auf Dreieck gestellt wird (DCO 1 Morph 0.00). Alle anderen Klangerzeuger (OSC 2, Sub, FM, Noise) werden stumm gestellt.
Gespielt wurde wiederum der Ton \(a'\). Im Gegensatz zum Sinuston des vorherigen Abschnitts wird die Dreieckschwingung als heller und schärfer empfunden. Auch hier gilt, dass der konstante Ton nach einigen Sekunden als störend wahrgenommen wird
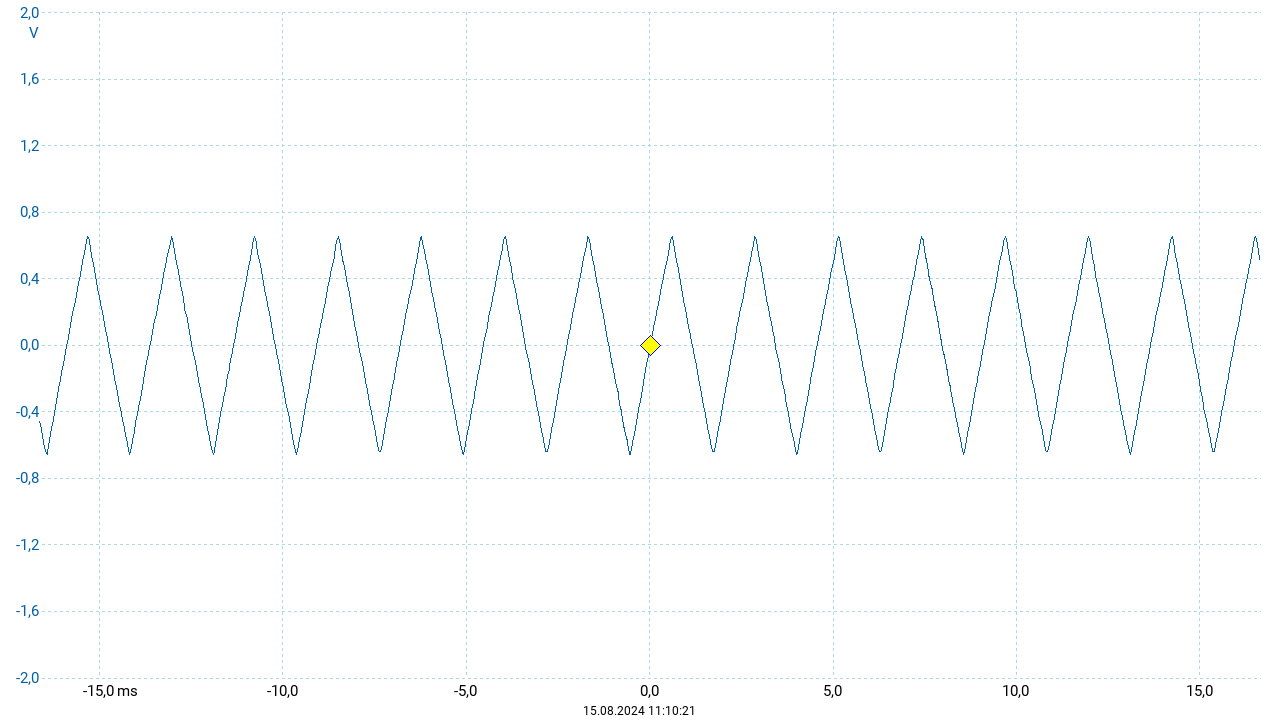
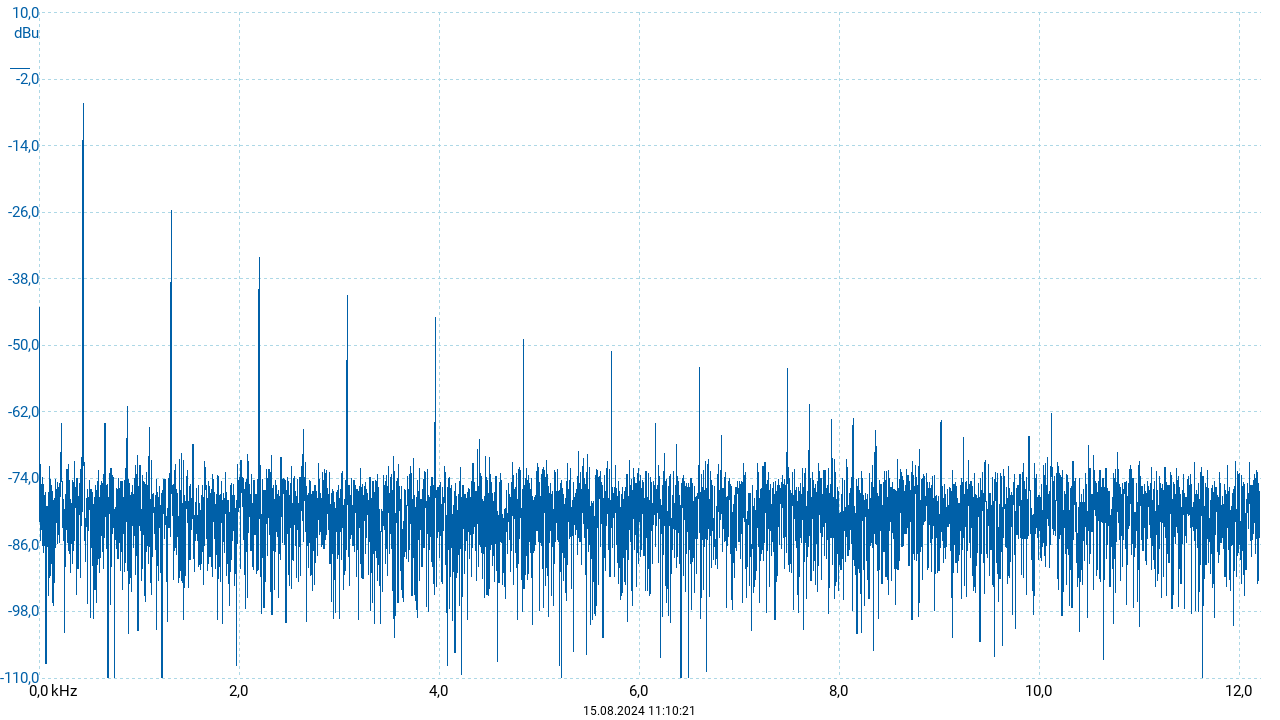
Das zugehörige Oszillogramm (obige Abbildung) zeigt die (aufgrund der Einstellungen erwartete) Dreieckform im zeitlichen Verlauf. Da es sich hierbei nicht um eine harmonische Schwingung handelt, enthält die Fouriertransformierte mehrere Peaks. Neben der Grundfrequenz, die weiterhin maßgeblich für die wahrgenommene Tonhöhe ist, treten höhere Frequenzen auf. Im Frequenzspektrum wurden die Position und die Höhen der einzelnen Peaks vermessen. Die Ergebnisse sind in der nachfolgenden Tabelle zu finden. Frequenz und Pegel wurden jeweils aus der Fouriertransformierten abgelesen. Die Frequenz ist dabei in Schritten von \(\Delta f \approx 1{,}5~\mathrm{Hz}\) diskretisiert. Die Nummer \(n\) der Harmonischen ergibt sich als ganzzahlig gerundetes Verhältnis der Peakfrequenz zur Frequenz des ersten Peaks. Das Amplitudenverhältnis (bezogen auf die gemessenen Spannungen) wurde aus den Pegeln bestimmt. Zum Vergleich ist für jede Harmonische der Wert \(\frac{1}{n^2}\) angegeben. Diese Zahlen entsprechen den Koeffizienten der Fourierreihe, die einer Dreieickschwingung zu Grunde liegt.
| \(n\) | \(f_\mathrm n \, / \, \mathrm{Hz}\) | \(L_\mathrm{V,n}\, / \, \mathrm{dB}\) | \(\frac{U_\mathrm n}{U_1}\) | \(\frac{1}{n^2}\) |
|---|---|---|---|---|
| 1 | 439,6 | -8,58 | 1 | 1 |
| 3 | 1320,2 | -27,83 | 0,1090 | 0,1111 |
| 5 | 2199,4 | -36,29 | 0,0412 | 0,0400 |
| 7 | 3080,1 | -42,91 | 0,0192 | 0,0204 |
| 9 | 3959,2 | -47,02 | 0,0120 | 0,0123 |
| 11 | 4839,9 | -51,30 | 0,0073 | 0,0083 |
| 13 | 5719,1 | -53,55 | 0,0056 | 0,0059 |
| 15 | 6598,2 | -57,08 | 0,0038 | 0,0044 |
Die Tabelle zeigt, dass bei der Dreieckschwingung neben der Grundfrequenz (erste Harmonische) nur die ungeradzahligen Vielfachen dieser Frequenz auftreten. Erwartungsgemäß folgen die Amplituden der einzelnen Harmonischen im Wesentlichen den Verhältnissen \(\frac{1}{n^2}\). Die Grundschwingung, die auch für die wahrgenommene Tonhöhe verantwortlich ist, hat die größte Amplitude. Die nachfolgenden Oberschwingungen fallen in ihren Amplituden rasch ab. Für die Klangfarbe sind sie dennoch wesentlich. Der hellere und schärfere Klang des Dreieckstons wird eben durch diesen Anteil der höheren Frequenzen hervorgerufen.
Weitere Schwingungsverläufe
Die Synth-One-App bietet als weitere elementare Schwingungsformen an: Rechteck, Puls, Sägezahn. Detaillierte Analysen wie oben für die Dreieckschwingung ließen sich für alle diese Formen durchführen, sollen an dieser Stelle jedoch nicht einzeln besprochen werden. Statt dessen erfolgen hier nur einige allgemeine Bemerkungen.
Für alle Verläufe, die keine reine Sinus- oder Kosinusschwingung darstellen, enthält das Frequenzspektrum mehrere Peaks, die mit wachsender Frequenz in ihrer Amplitude abfallen. Die einzelnen Schwingungsformen unterscheiden unterscheiden sich insbesondere darin,
- ob alle Oberschwingungen, oder nur (un-) geradzahlige auftreten sowie
- wie schnell die Amplituden der Oberschwingungen mit wachsender Frequenz abnehmen.
Für den Klang dieser Schwingungsformen lassen sich die bisher getroffenen Aussagen weiterführen: Je reicher ein Klang an Obertönen ist (d.h. höhere Anzahl und/oder größere Amplituden der Obertöne) desto heller und schärfer wird er empfunden.
Überlagerung von Schwingungen
Werden zwei (Sinus-) Töne der Form
\[\begin{aligned} a_1(t) & = a_0 \sin(2\pi f_1 t) \quad \textrm{und} \\ a_2(t) & = a_0 \sin(2\pi f_2 t) \end{aligned}\]
gleichzeitig gespielt, so überlagern sich ihre Schwingungen additiv. Die jeweilige Anfangsphase wurde in den obigen Formeln aus Gründen det Übersichtlichkeit nicht beücksichtigt. Aus den Rechenregeln für Winkelfunktionen folgt die Äquivalenz folgender Ausdrücke:
\[a_\mathrm{max} \left[ \sin(2\pi f_1 t) + \sin(2\pi f_2 t)\right] = 2a_\mathrm{max} \sin\left(2\pi \frac{f_1 + f_2}{2} t\right) \cos\left(2\pi \frac{f_1 - f_2}{2} t\right) \, .\]
Für die Überlagerung von Schwingungen bietet die Synth-One-App zwei Herangehensweisen:
- Bei Verwendung eines Schwingungserzeugers (OSC 1 / 2, FM, Noise) werde gleichzeitig verschiedene Töne auf der Klaviatur gespielt.
- Es werden zwei unterschiedliche Schwingungserzeuger aktiviert.
Im ersten Fall lassen sich nur die musikalischen Intervalle entsprechend der Halbtonschritte realisieren. Im zweiten Fall sind durch die Möglichkeit der „Verstimmung“ einzelner Schwingungserzeuger beliebige Frequenzkombinationen möglich. Selbstverständlich ist auch eine Kombination beider Herangehensweisen möglich: bei mehreren aktivierten Schwingungserzeugern werden mehrere Töne gleichzeitig gespielt.
Musikalische Intervalle
Musikalische Intervalle werden nach der Anzahl der Schritte auf der Tonleiter benannt. Für die Betrachtungen in diesem Abschnitt wird jeweils der Ton \(c'\) mit der Frequenz \(f_{c'} = 261{,}6~\mathrm{Hz}\) als Ausgangspunkt verwendet. Den nächsthöheren Ton C (\(c''\)) erhält man nach acht Tonleiterschritten. Dieses Intervall wird als Oktave bezeichnet. Die nachfolgenden Abbildungen zeigen die Überlagerung dieser beiden Töne als Schwingungsverlauf und Frequenzspektrum.
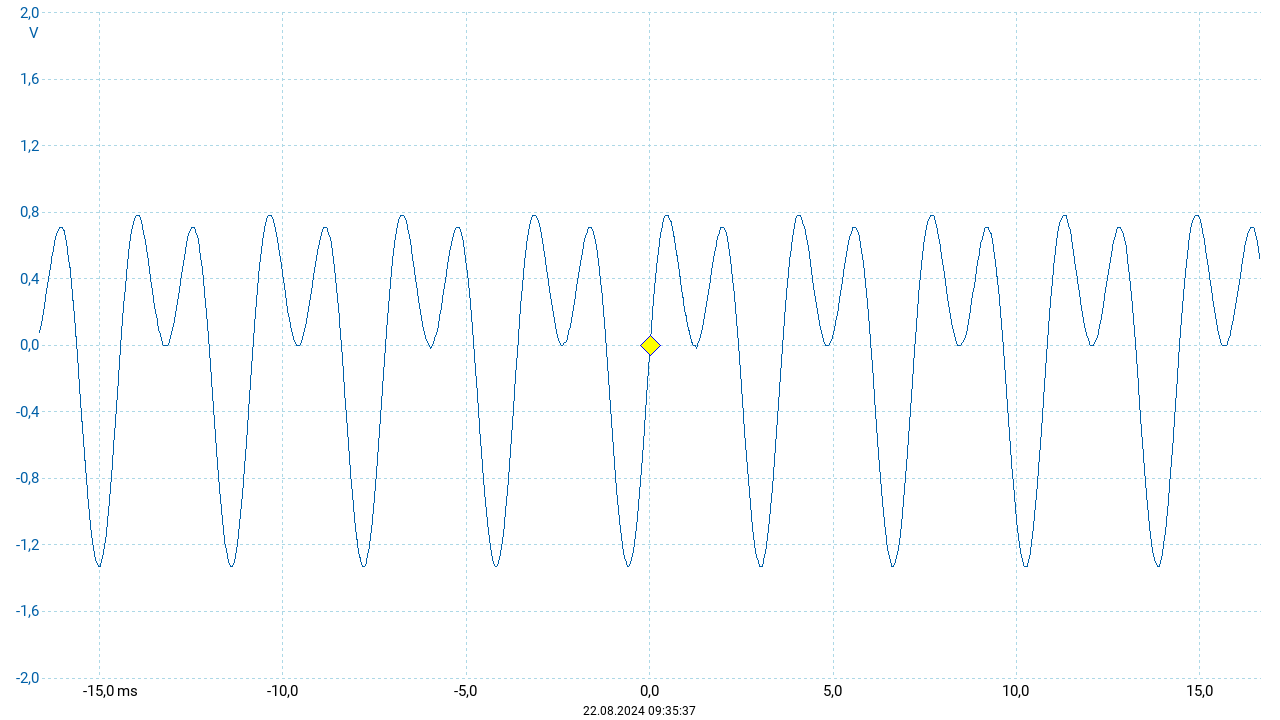
Eine Oktave bedeutet die Verdopplung der Frequenz. Die obigen Verläufe entsprechen der Überlagerung zweier Schwingungen mit den Frequenzen \(f\) und \(2f\). Der Unterschied zwischen den beiden Verläufen ist die Phasenlage zwischen den beiden Schwingungen. Werden die beiden Töne nacheinander angespielt, so ergibt sich eine Phasenverschiebung zwischen ihnen. Auf den Klang des Intervalls hat dies jedoch keinen Einfluss. Auch im Frequenzspektrum lässt sich die Phasenverschiebung nicht ablesen. Die Fouriertransformation liefert eine komplexwertige Funktion \(A(f)\), deren Werte durch Betrag und Phase gekennzeichnet sind. Im Frequenzspektrum werden nur die Beträge von \(A(f)\) dargestellt. Die Phaseninformation bleibt in dieser Darstellung unberücksichtigt.
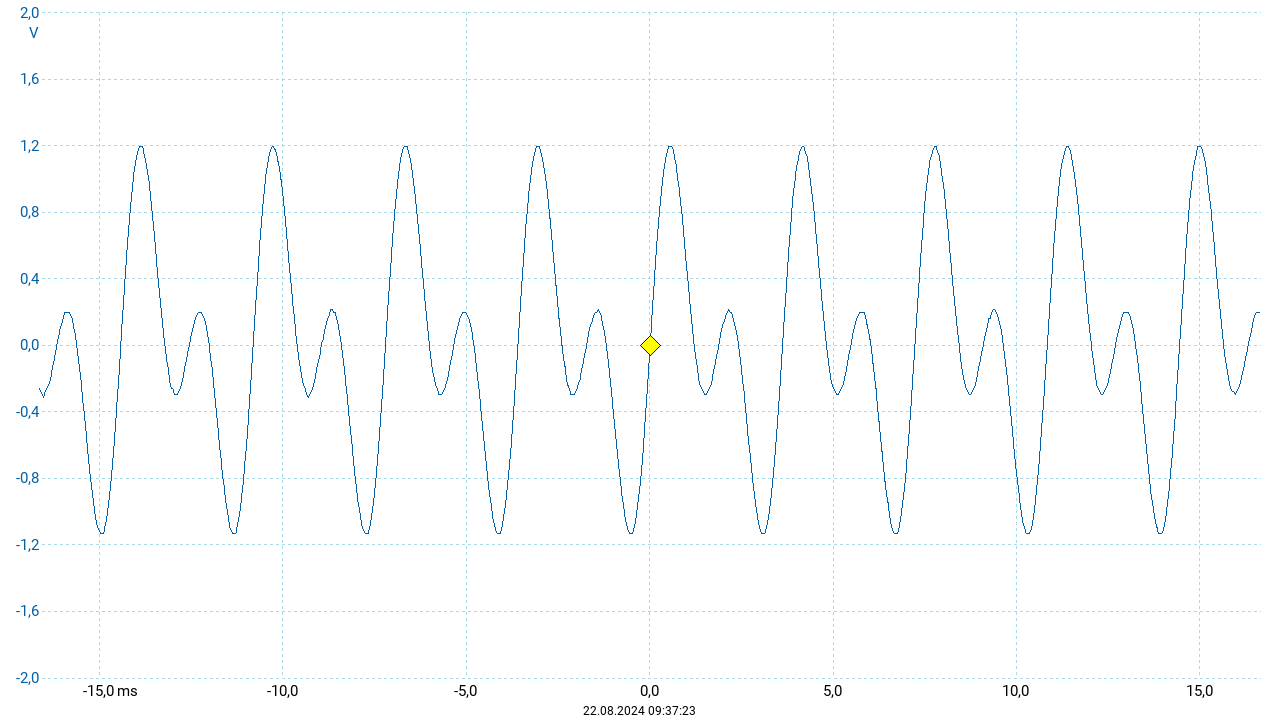
Das Intervall der Oktave erzeugt einen als angenehm empfundenen Zusammenklang der Töne. Begründet ist dies im einfachen (d.h. kleinen ganzzahligen) Frequenzverhältnis von \(2:1\). Der entstehende Schwingungsverlauf wiederholt sich unverändert mit der Frequenz des tieferen Tons. Hiervon ausgehend können „wohlklingende“ Intervalle anhand der Frequenzverhältnisse gesucht werden. Als nächsthöheres Verhältnis ergibt \(3:2\), was musikalisch zum Intervall der Quinte führt. Ausgehend vom Ton \(c'\) erhält man als Quinte den Ton \(g'\). Diagramme dieses Zusammenklangs sind in der nachfolgenden Abbildung zu sehen.
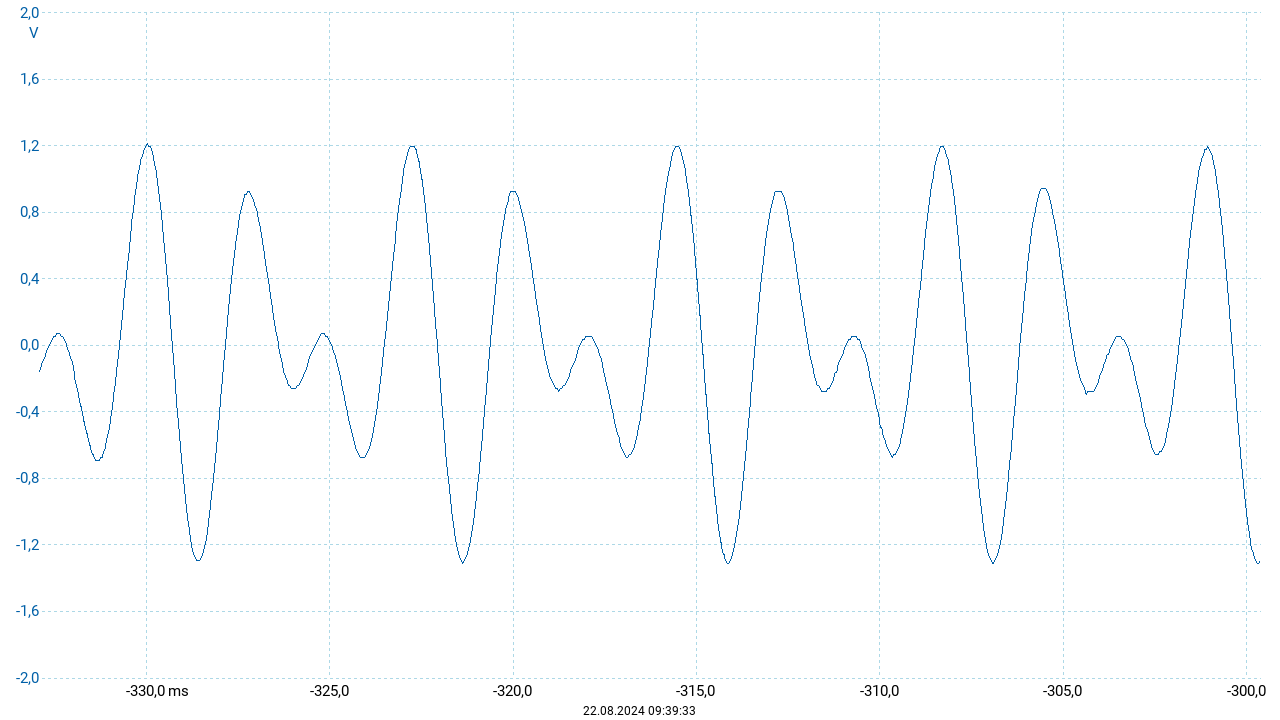
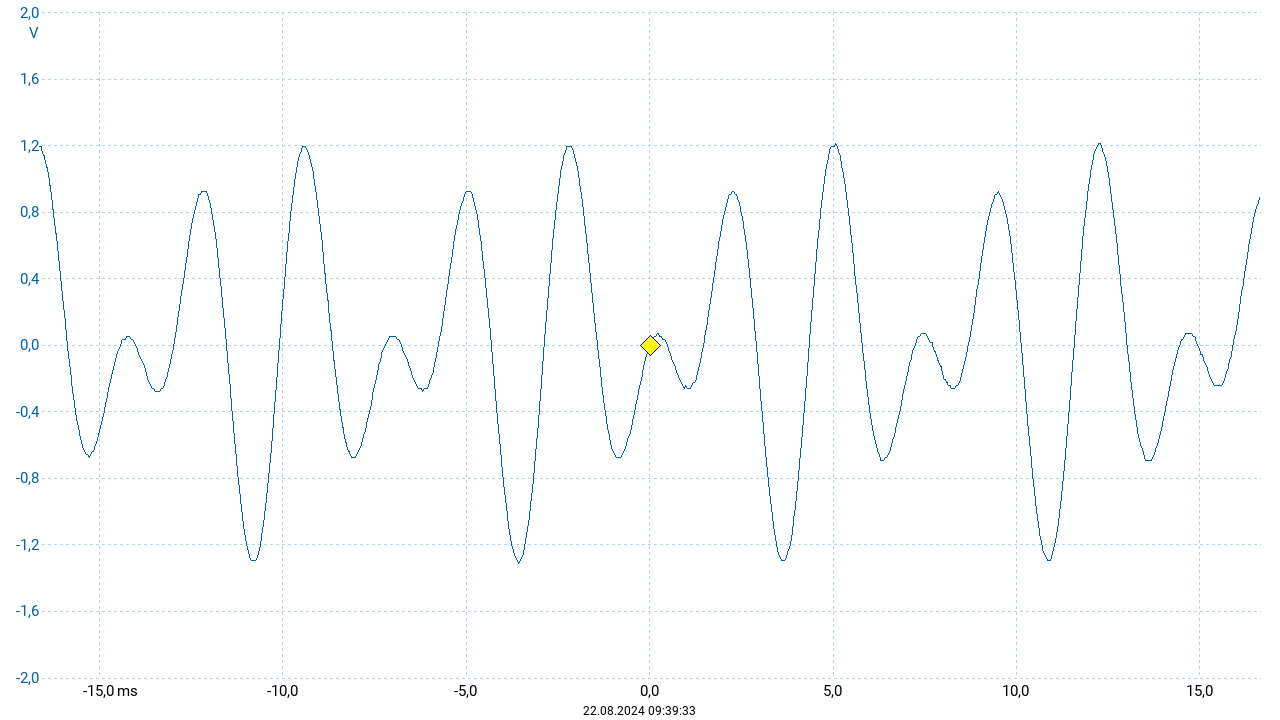
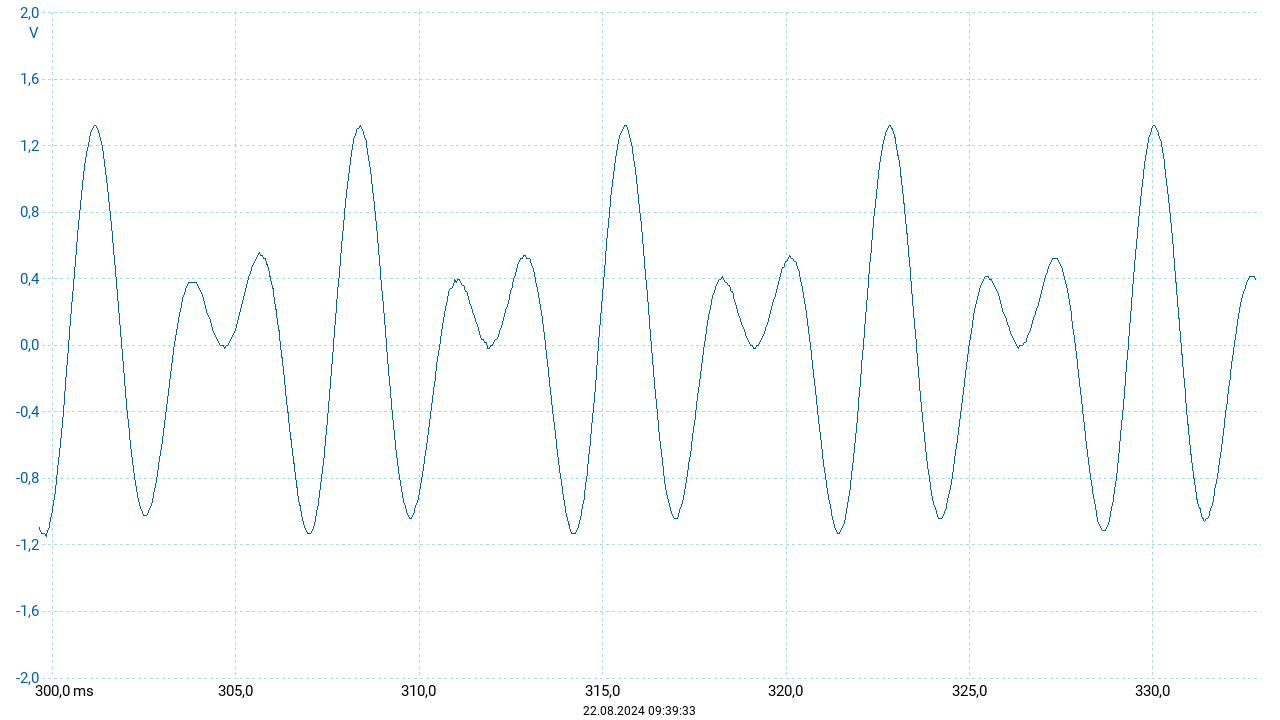
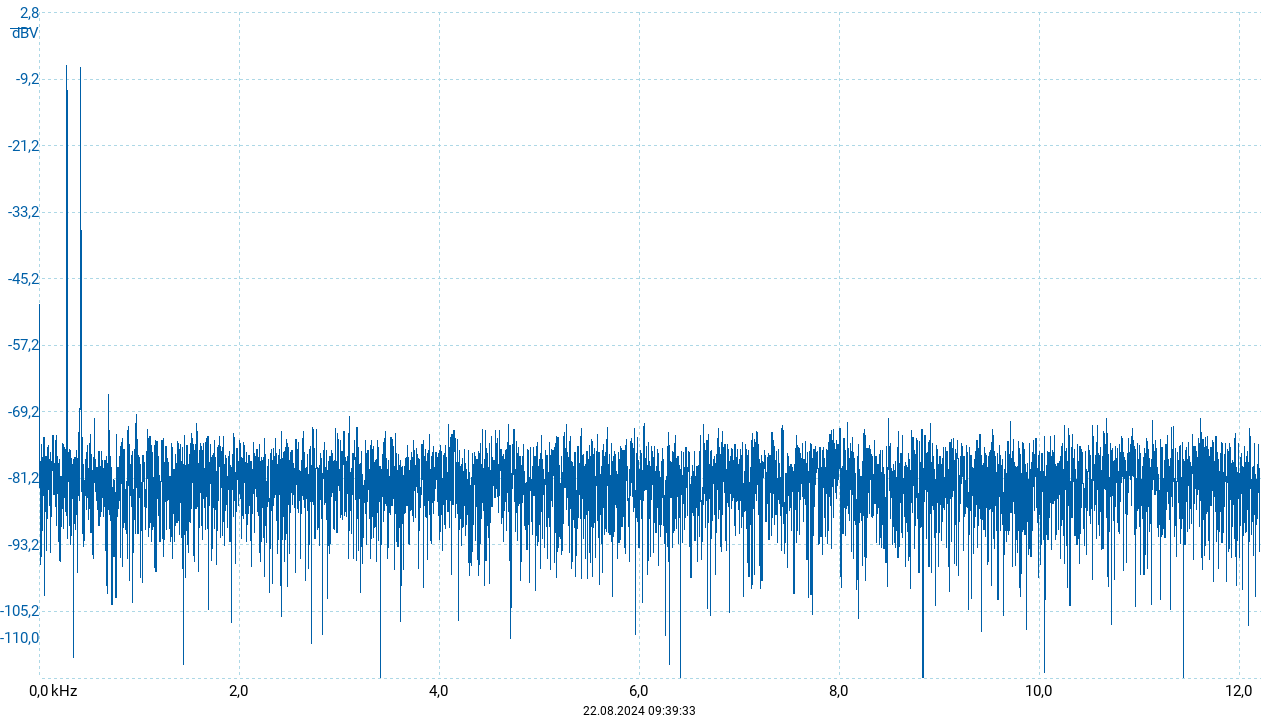
Für die obigen Darstellungen wurde der entstehende Ton über eine Dauer vor \(667~\mathrm{ms}\) aufgezeichet. Die drei Oszillogramme sind Ausschnitte dieser Aufnahme aus unterschiedlichen Zeitpunkten. Überraschenderweise zeigt der Vergleich dieser drei Darstellungen, dass sich der Verlauf der resultierenden Schwingung während dieser Zeit ändert. Für das oben angegebene Frequenzverhältnis \(3:2\) müsste sich ein Verlauf ergeben, der sich nach 2 Periodendauern des tieferen Tons (entsprechend 3 Periodendauern des höheren Tons) unverändert wiederholt. Die obigen Darstellungen weisen auf eine zusätzliche Phasenverschiebung hin, die durch eine geringe Abweichung vom ganzzahligen Verhältnis \(3:2\) entsteht. Tatsächlich sind Instrumente zumeist nicht „rein“ (also mit den exakten Quinten von \(3:2\)) gestimmt, sondern gleichstufig. Dabei wird für jeden Halbtonschritt die Frequenz um denselben Faktor erhöht beziehungsweise vermindert. Um nach zwölf Halbtonschritten (entsprechend einer Oktave) die doppelte Frequenz zu erreichen, muss dieser Faktor \(\sqrt[12]2\) betragen. Die Quinte umfasst sieben Halbtonschritte. Ihre Frequenz ist folglich um den Faktor \(2^\frac{7}{12} \approx 1{,}4983\) größer als der Ausgangston.
Als weitere grundlegende Intervalle sollen die Terzen behandelt werden. Die nachfolgende Abbildung zeigt den Schwingungsverlauf der großen Terz \(c'\) – \(e'\) sowie der kleinen Terz \(c'\) – \(es'\). In reiner Stimmung entsprechen die Terzen den Frequenzverhältnissen \(5:4 = 1{,}25\) (große Terz) beziehungsweise \(6:5 = 1{,}2\) (kleine Terz). In der hier verwendeten gleichstufigen Stimmung ergeben sich Verhältnisse von \(\sqrt[3]{2}:1 \approx 1{,}2599\) (große Terz) beziehunsgweise \(\sqrt[4]{2}:2 \approx 1{,}1892\) (kleine Terz).
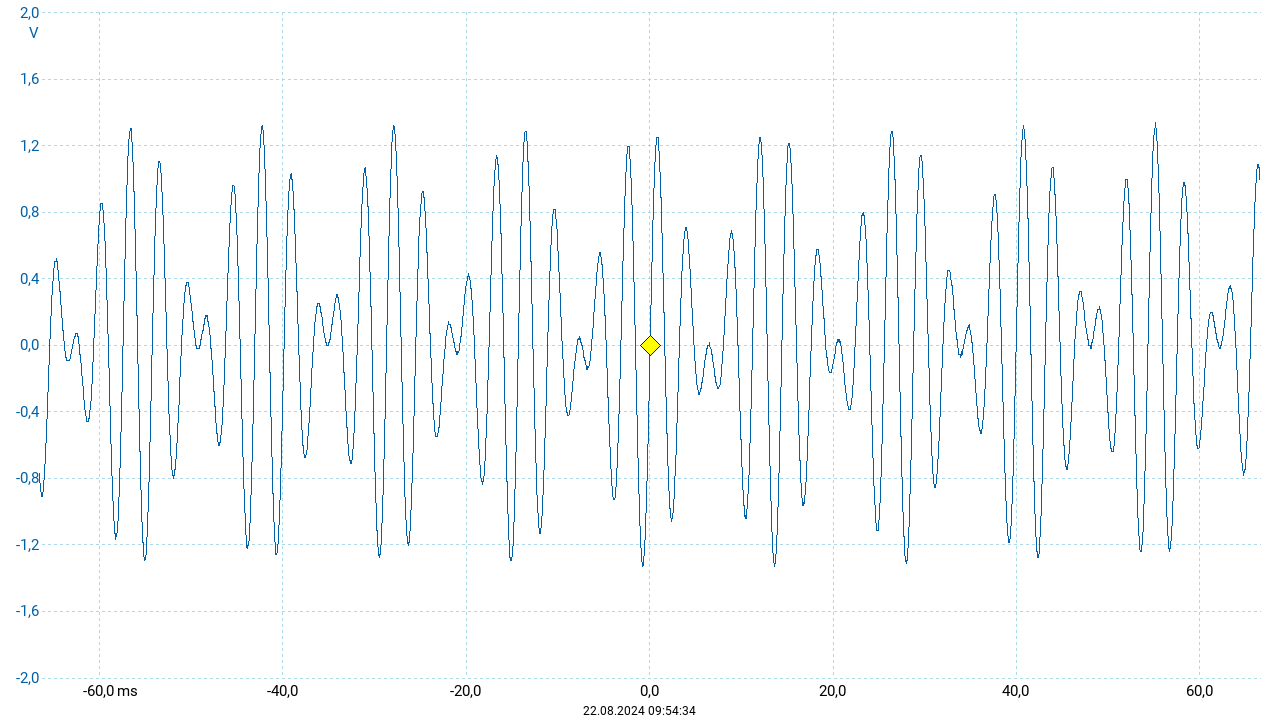
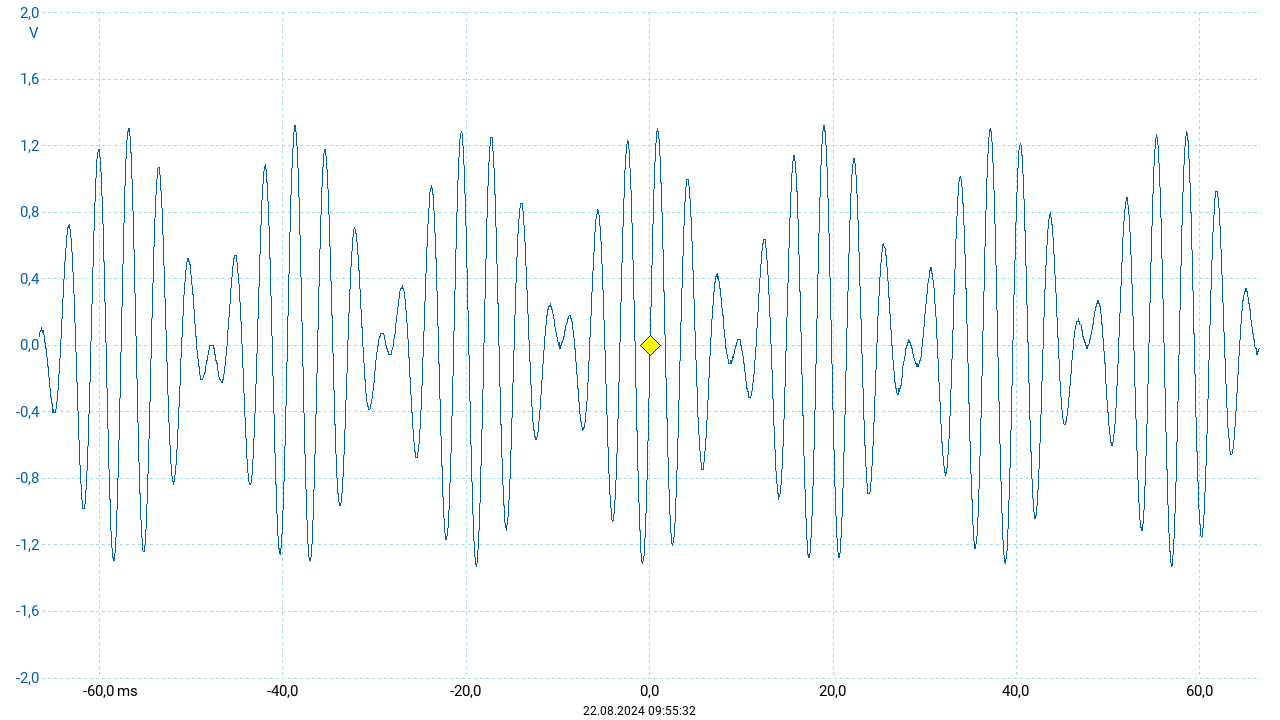
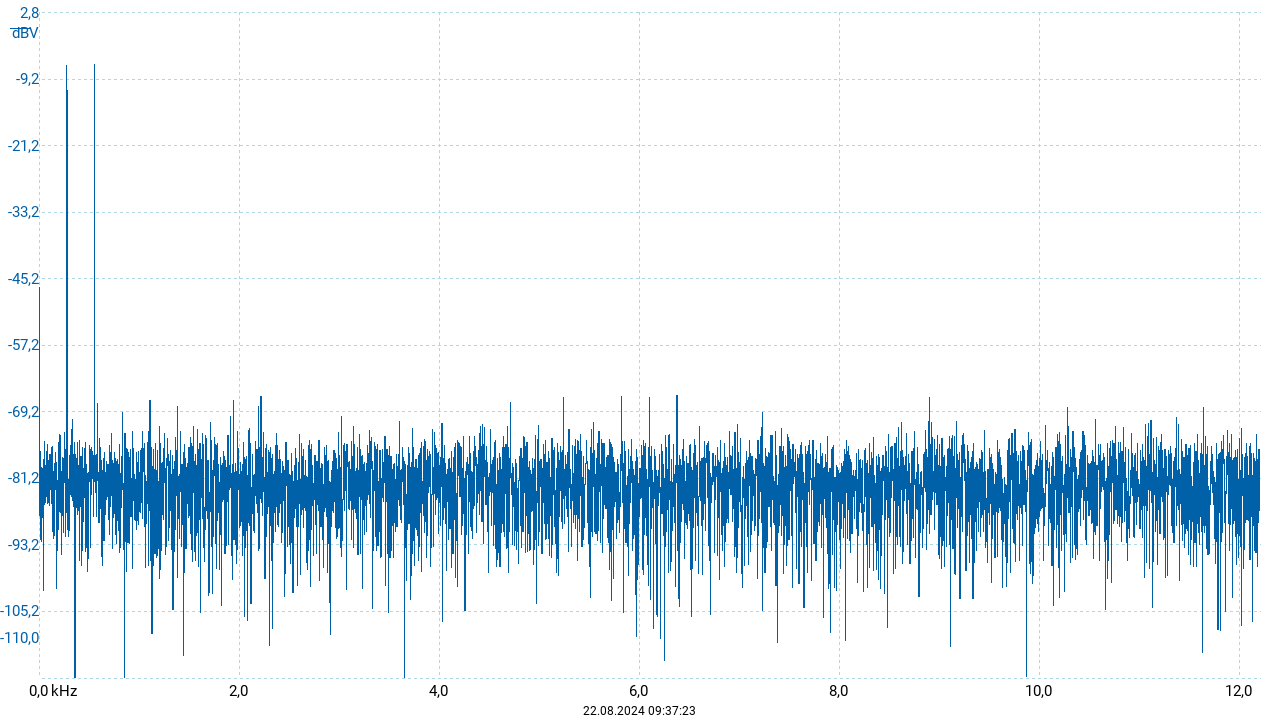
Während bei den vorherigen Beispielen die additive Überlagerung der beteiligten noch im Kurvenverlauf erkennbar war, zeigt sich bei den hier auftretenden Frequenzverhältnissen ein anderes Erscheinungsbild der resultierenden Schwingung: Das Oszillogramm erscheint als Schwingung einer Frequenz, die in regelmäßigen Zeitabständen Maxima und Minima ihrer Amplitude durchläuft. Diese Form entspricht der rechten Seite der oben angegebenen Äquivalenz der Winkelfunktionen: Die (Sinus-) Schwingung der Frequenz \(\frac{1}{2}(f_1 + f_2)\) wird durch eine (Kosinus-) Schwingung der Frequenz \(\frac{1}{2}(f_1 - f_2)\) moduliert. Je näher die beiden Frequenzen beieinander liegen, desto kleiner wird die Modulationsfrequenz. Das Frequenzspektrum (siehe nachfolgende Abbildung) zeigt stets die additiven Komponenten der Schwingung. So sind auch hier zwei Peaks entsprechend der Frequenzen der beiden Einzeltöne zu sehen.
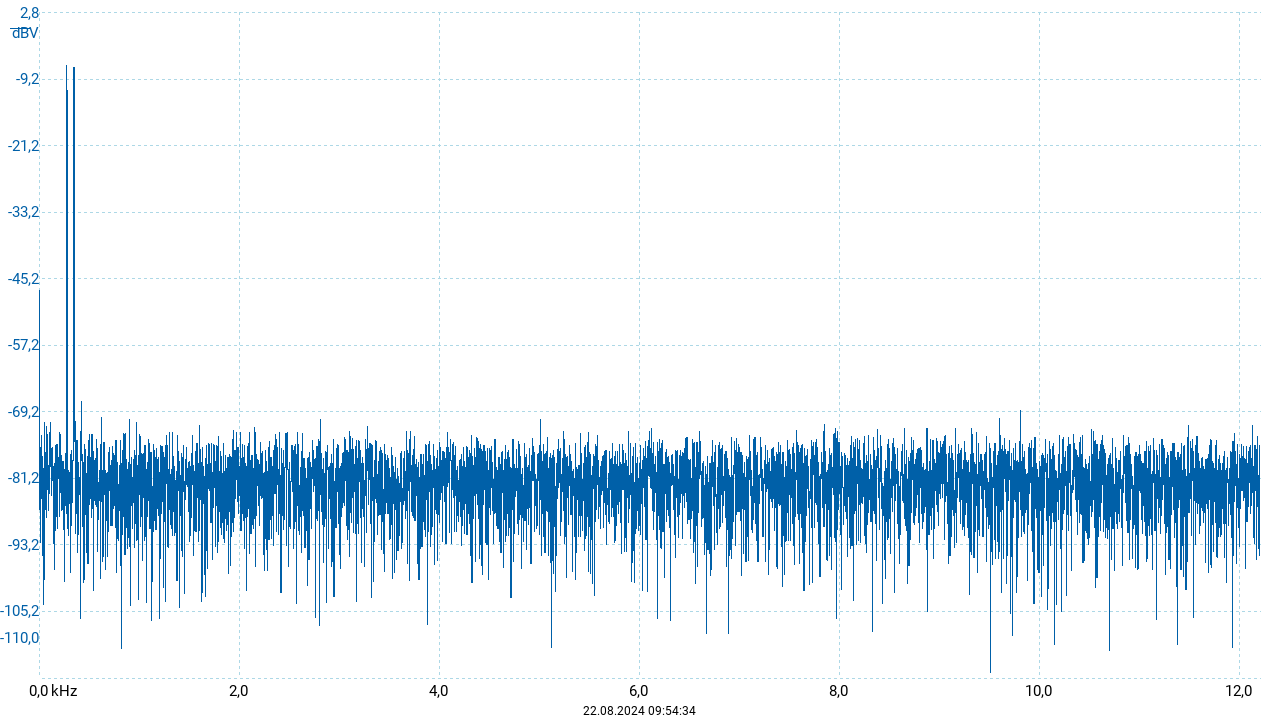
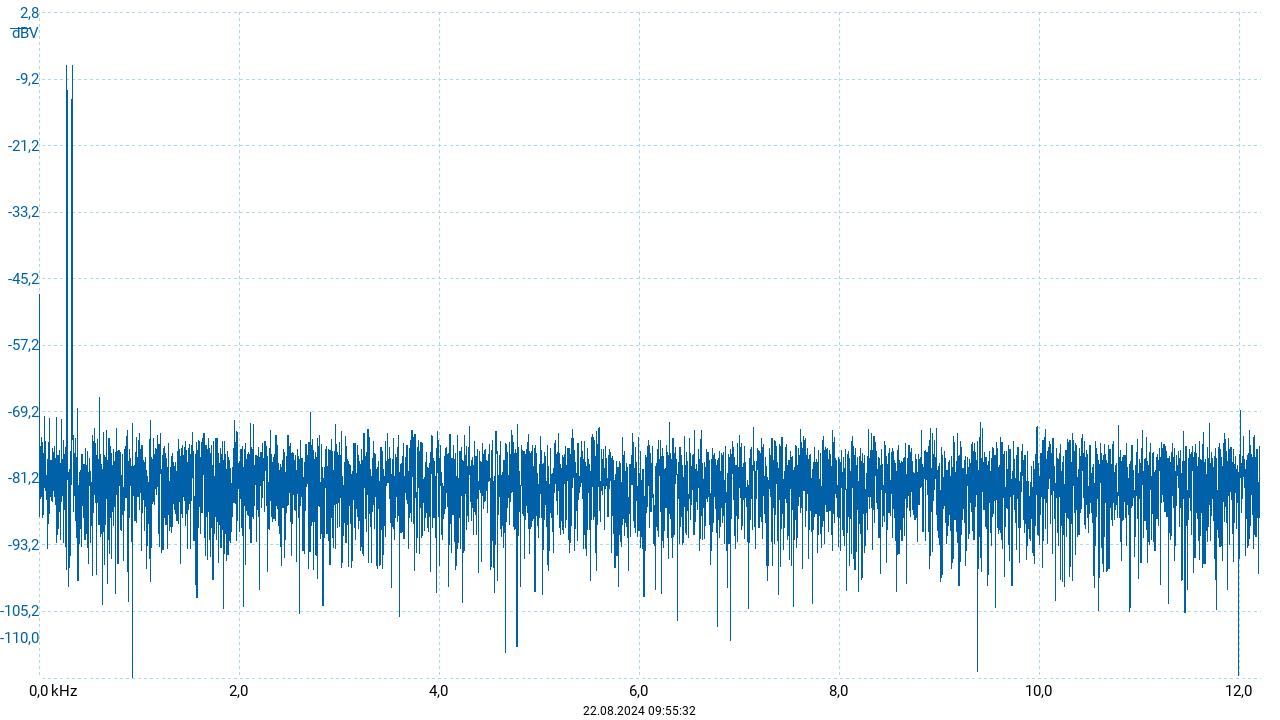
In der Wahrnehmung erscheinen die Terzen aufgrund des kleineren Frequenzverhältnisses etwas weniger wohlklingend als die Quinte. Außerdem werden große und kleine Terz unterschiedlich empfunden. So ist die große Terz für den hellen und fröhlichen Charakter des Dur-Dreiklangs (\(c\) – \(e\) – \(g\)) verantwortlich, während die kleine Terz dem Moll-Dreiklang (\(c\) – \(es\) – \(g\)) einen trüben, traurigen Charakter verleiht.
Schwebung
Wie oben bereits festgestellt führt die Überlagerung zweier Schwingungen mit geringem Frequenzunterschied zur Ausbildung einer Resultierenden, deren Amplitude periodische Minima und Maxima aufweist. Bei den oben behandelten Terzen betrugen die Zeitabstände zwischen aufeinanderfolgenden Minima weniger als \(20~\mathrm{ms}\), was unterhalb der menschlichen Wahrnehmungsmöglichkeiten liegt. Wird der Frequenzunterschied der überlagernden Wellen jedoch klein genug gewählt, so werden die Zeitdauern zwischen den Amplitudenmaxima beziehunsgweise -minima so groß, dass sie als An- und Abschwellen eines Tons wahrgenommen werden können. Dieser Effekt wird als Schwebung bezeichnet.
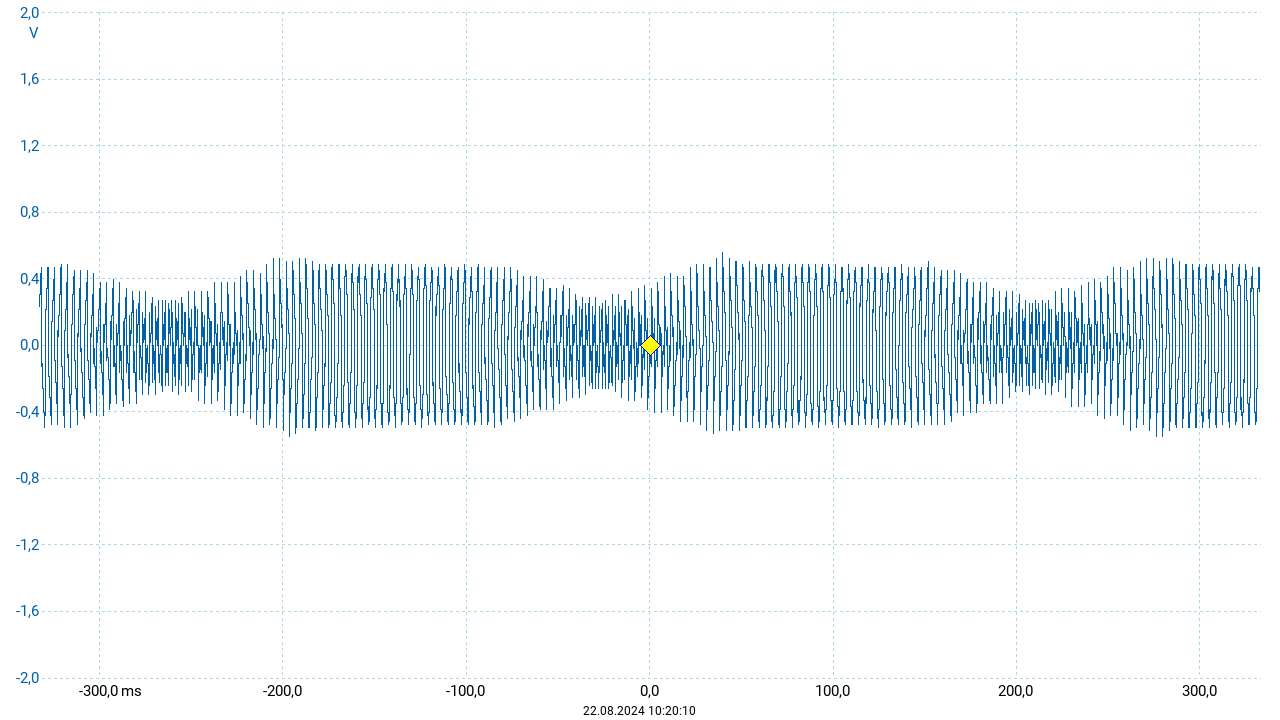
Mit der hier verwendeten App lassen sich nicht zwei unabhängige Sinusschwingungen erzeugen. Daher wird hier zunächst mit zwei Dreieckschwingungen gearbeitet. Dafür sind die beiden „Oszillatoren“ (OSC 1 & OSC 2) jeweils auf Dreieck eingestellt. Ihre Lauststärken (Abschnitt Volume) sind auf identische Werte und der Mix auf \(0{,}5\) eingestellt. Alle anderen Tonerzeuger sind inaktiv. Bei OSC 2 ist zusätzlich das Detune auf den Maximalwert \(4{,}0\) eingestellt. Dieser Oszillator erzeugt somit eine um \(4~\mathrm{Hz}\) höhere Frequenz. Mit diesen Einstellungen wurde der Ton \(c'\) gespielt. Der resultierende Schwingungsverlauf ist in der nachfolgenden Abbildung gezeigt.
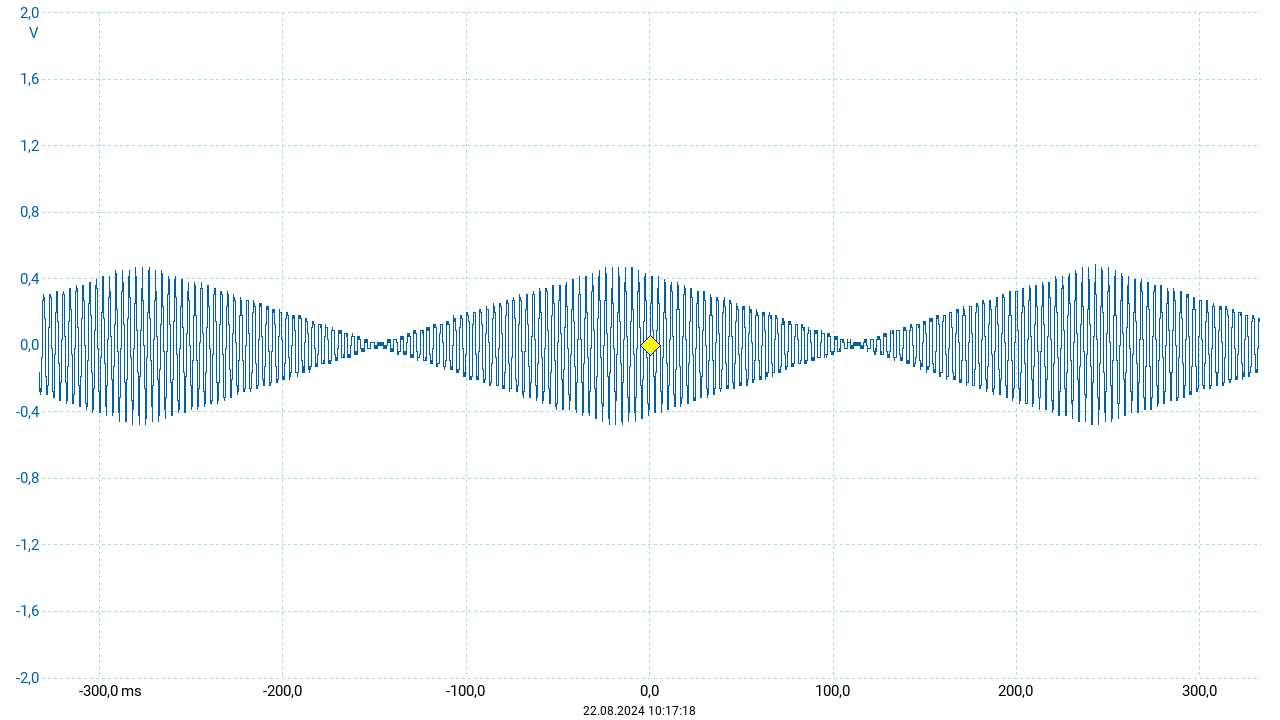
Das Oszillogramm zeigt das periodische An- und Abschwellen der Amplitude. Die Einhüllende hat die Frequenz \(\frac{1}{2}\left|f_1 - f_2\right|\), was in diesem Fall \(2~\mathrm{Hz}\) ergibt. Die Schwebungsfrequenz, d.h. die Frequenz, mit der Minima beziehungsweise Maxima aufeinander folgen, ist das Doppelte der Frequenz der Einhüllenden und smit identisch zur Differenzfrequenz der beiden Einzelschwingungen, hier \(f_\mathrm{schwebung} = 4~\mathrm{Hz}\). Daraus ergibt sich eine Periodendauer der Schwebung von \(250~\mathrm{ms}\), was auch in der obigen Darstellung abgelesen werden kann.
Ursache der Schwebung ist eine sich periodisch ändernde Phasenverschiebung \(\Delta\phi\) zwischen den beteiligten Schwingungen. Sind beide Schwingungen phasengleich (\(\Delta\phi=0\)) so fallen Maximum auf Maximum und Minimum auf Minimum. Hier zeigt die resultierende Amplitude ein Maximum. Nach einer halben Periodendauer der Schwebung verlaufen beide Schwingungen gegenphasig (\(\Delta\phi = \pi\)) und es fallen Maximum auf Minimum und umgekehrt. Da beide Einzelschwingungen identische Amplituden (und ein identisches Obertonspektrum) aufweisen, sinkt die resultierende Amplitude auf Null ab.
Im Frequenzspektrum zeigt sich die Schwebungsfrequenz nicht. Dort sind alle additiven Komponenten abzulesen, jedoch nicht die daraus resultierende Einhüllende. Da hier zwei Dreieckschwingungen überlagert wurden, zeigt auch das Frequenzspektrum im Wesentlichen eine Peakfolge, wie sie weiter oben bereits für eine einzelne Dreieckschwingung untersucht wurde. Durch die Überlagerung stehen in diesem Fall nun an jeder Position zwei Peaks mit der entsprechenden Frequenzdifferenz.
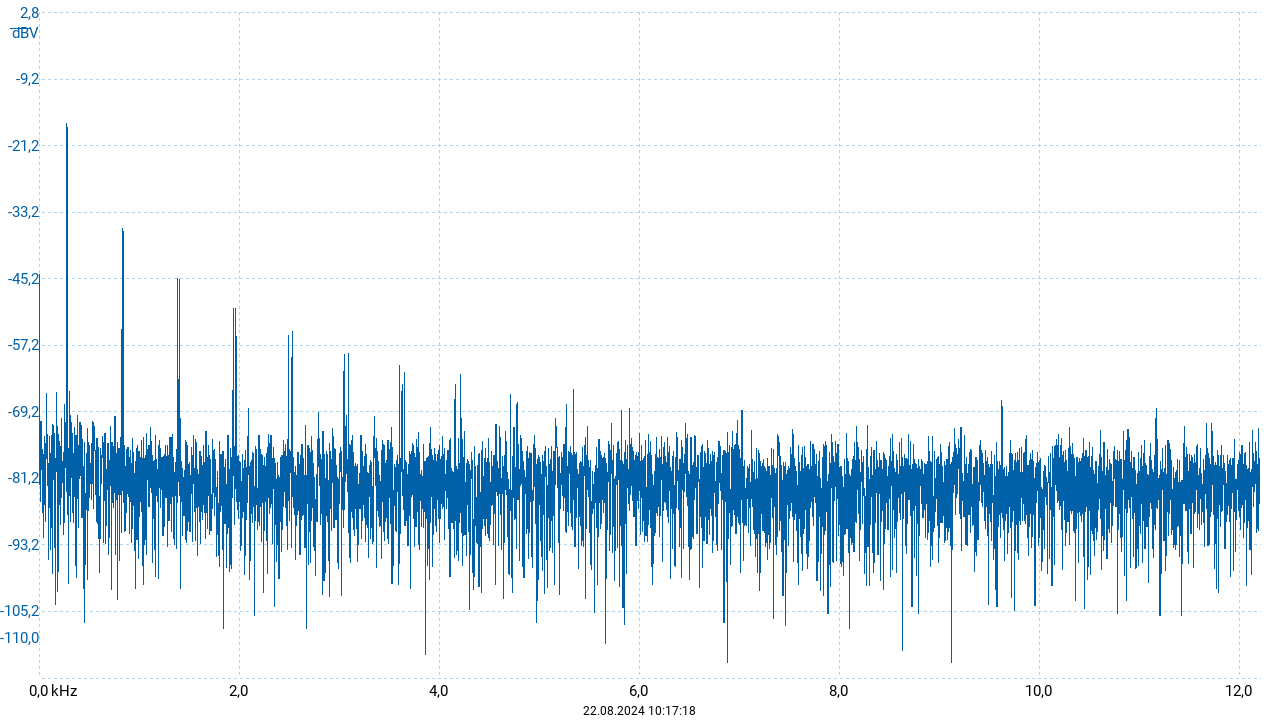
Die Synthesizer-App erlaub auch die Überlagerung unterschiedlicher Schwingungsverläufe. Ausgehend vom vorigen Beispiel wurde OSC 2 auf eine Rechteckschwingung eingestellt. Alle anderen Parameter blieben unverändert. Wiederum wurde der Ton \(c'\) gespielt. Die resultierende Schwingung ist in der folgenden Abbildung gezeigt.
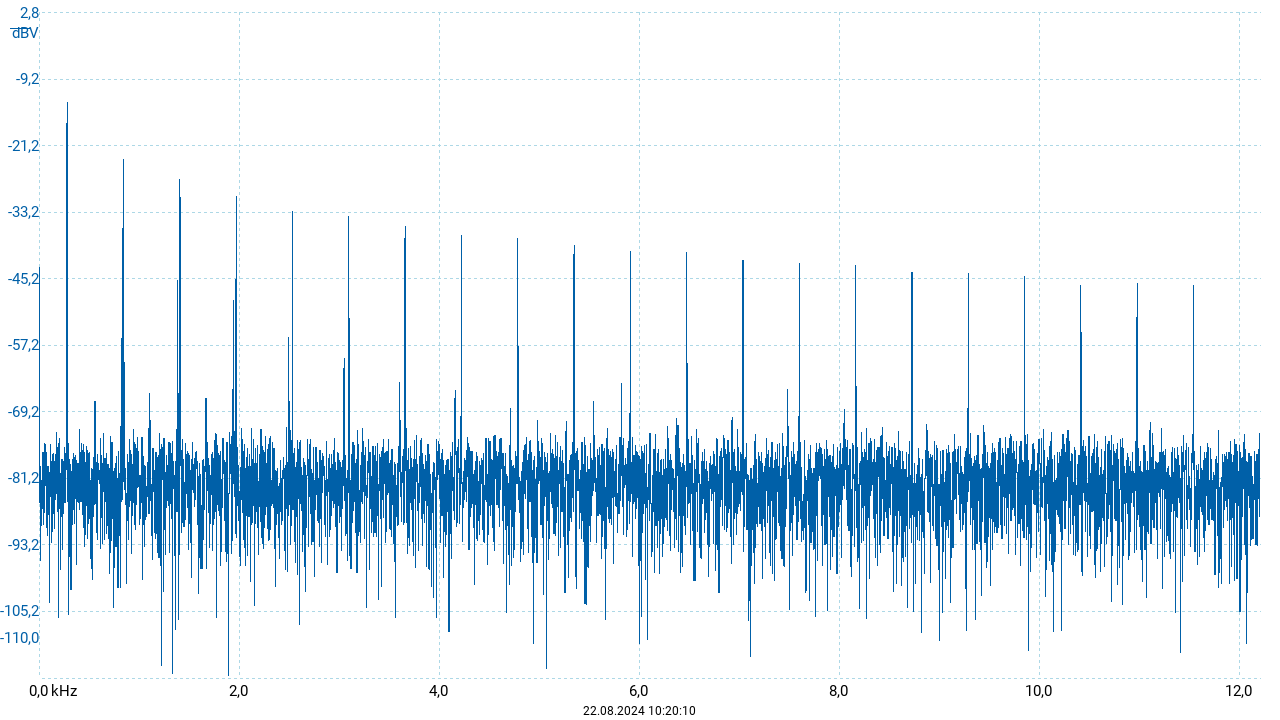
Aufgrund der Frequenzverschiebung entsteht auch hier eine Schwebung mit einer Periodendauer von \(250~\mathrm{ms}\). Allerdings weisen in diesem Fall die beiden Einzelschwingungen ein unterschiedliches Obertonspektrum auf. So kommt es auch bei gegenphasigem Verlauf der beiden Einzelschwingungen nicht zu einer vollständigen Auslöschung der (Gesamt-) Amplitude.
Im zugehörigen Frequenzspektrum lassen sich die Unterschiede im Obertonspektrum ablesen. Beide Schwingungsformen setzen sich zusammen aus der Grundfrequenz und ihren ungeradzahligen Peakpositionen. (Zusätzlich erscheinen kleinere Peaks die mathematisch zu keiner der beiden Schwingungen gehören und als Artefakt dieser App auftreten). An den einzelnen Peakpositionen erscheinen jeweils zwei unterschiedlich hohe Peaks, wobei der jeweils linke Peak (kleinere Frequenz) in diesem Fall zur Dreieckschwingung (OSC 1, ohne Detune) und der jeweils rechte Peak (höhere Frequenz) zur Rechteckschwingung (OSC 2, Detune \(+4~\mathrm{Hz}\)) gehört. Wie in der Darstellung zu erkennen ist, treten bei der Rechteckschwingung die Obertöne mit größerer Amplitude auf als bei der Dreieckschwingungen. Mathematisch ergibt sich die Amplitude der \(n\)-ten Harmonischen bei der Dreieckschwingung zu \(\frac{1}{n^2}\), bei der Rechteckschwingung hingegen zu \(\frac{1}{n}\). In der Folge sind bei den höheren Frequenzen (etwa rechte Hälfte des Frequenzspektrums) nur noch die zur Rechteckschwingung gehörigen Peaks erkennbar.
Ausblick
Die Möglichkeiten, die Synthesizer für die musikalische Gestaltung oder eben – wie in diesem Bericht – für physikalische Untersuchungen bieten, sind schier endlos. In den bisherigen Abschnitten wurde nur wenige elementare Funktionen benutzt. Für weitere Schritte bietet sich beispielsweise die Untersuchung der Wirkung von Filtern (Hoch-, Tief- oder Bandpass) an. Für die klangliche Gestaltung ist darüber hinaus die Beeinflussung des zeitlichen Verlaufs eines Tons maßgeblich, die bisher vollkommen unbeachtet blieb. Doch auch dies sind lediglich Grundfunktionalitäten eines Synthesizers. Fortgeschrittenere Features warten dann immer noch auf ihre (klangliche und physikalische) Untersuchung.
All diese Dinge in einen einzigen Bericht zu packen, würde den Rahmen sprengen. So bleibt am Ende dieses Berichts die Feststellung, dass es wohl das Beste ist, selbst mit dem Probieren und Experimentieren zu beginnen, und die weiteren Kapitel selbst zu entdecken…
Quellenverzeichnis
Diskrete Fourier-Transformation auf https://de.wikipedia.org (abgerufen am 26.08.2024 11:02 Uhr)↩︎
Sam MacGuire und Nathan Van der Rest, The Musical Art of Synthesis, Focal Press 2016↩︎
Francis Preve, Audiokit Synth One The Ultimate Guide, E-Book als PDF (https://audiokitpro.com/images/AudioKitSynthOne-Guide.pdf) oder via Apple Books↩︎
