Bestimmung der Brechzahl von Wasser
Aufgabenstellung
Zur Bestimmung der Brechzahl n_\mathrm W von Wasser wird folgendes Experiment durchgeführt (siehe Abbildung): Über einem hohen Standzylinder aus Glas befindet sich ein Laser-Entfernungssensor. Dieses Messgerät sendet Lichtpulse aus, die am angepeilten Objekt reflektiert werden und zurück in den Sensor gelangen. Der Sensor misst die Laufzeit des Lichts von der Aussendung bis zur Rückkehr des reflektierten Lichts.
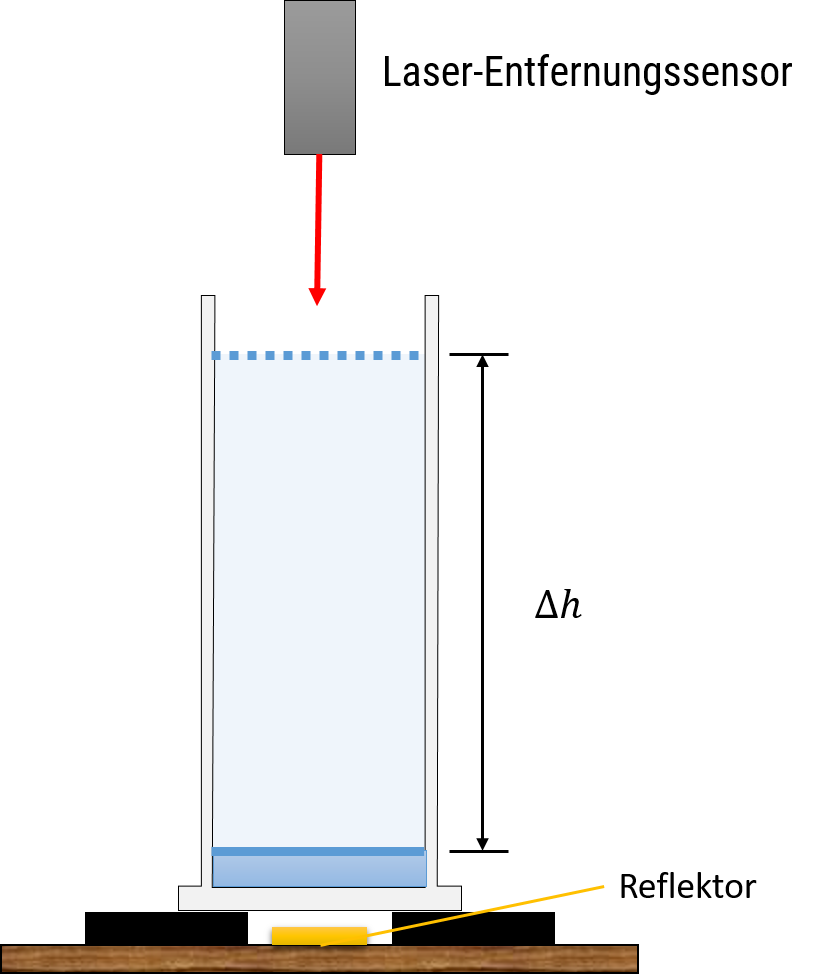
Der Laserstrahl dieses Messgerätes ist auf eine Reflektorscheibe gerichtet, die sich unter dem Standzylinder befindet. Zunächst ist im Zylinder nur der Boden etwas mit Wasser bedeckt. Der Lasersensor bestimmt dabei eine Laufzeit von t_1=5{,}18~\mathrm{ns}. Nun wird Wasser in den Standzylinder gefüllt, sodass der Wasserspiegel um \Delta h=30~\mathrm{cm} angehoben wird. Die Laufzeit des Lichts beträgt am Ende der Befüllung t_2=5{,}92~\mathrm{ns}. Bestimmen Sie daraus den Brechungsindex von Wasser n_\mathrm W (der Brechungsindex von Luft hat den Wert n_\mathrm L=1).
Lösung
Der Laufweg des Lichts lässt sich in zwei Anteile aufspalten:
s_\mathrm W=2\Delta h: Die Strecke, um die der Wasserspiegel steigt. Zu Beginn legt das Licht diesen Weg durch Luft zurück, am Ende des Experiments durch Wasser. Da das Licht den Standzylinder zweimal passiert (Hin- und Rückweg) ist die Höhendiffernz doppelt zu berücksichtigen.
s_\mathrm R: Die gesamte restliche Strecke durch Glas, Luft und die Anfangsmenge an Wasser. Für diese Strecke tritt keine Veränderung ein.
Der gesamte zurückgelegte Weg ist dann s_\mathrm{ges}=s_\mathrm W + s_\mathrm R.
Die Laufzeit des Lichts lässt sich in analoger Weise in die beiden Anteile t_\mathrm W und t_\mathrm R aufteilen: t_\mathrm{ges}=t_\mathrm W +t_\mathrm R.
Zu Beginn des Experiments:
t_1= t_\mathrm{W(Luft)}+t_\mathrm R und am Ende des Experiments:
t_2= t_\mathrm{W(Wasser)}+t_\mathrm R
Für die Zeitdifferenz
t_2-t_1= t_\mathrm{W(Wasser)}+t_\mathrm R-(t_\mathrm{W(Luft)}+t_\mathrm R)=t_\mathrm{W(Wasser)}- t_\mathrm{W(Luft)} ist dabei nur die Teilstrecke s_\mathrm W relevant. Für deren zugehörige Laufzeit gilt am Anfang des Experiments:
t_\mathrm{W(Luft)}=\frac{s_\mathrm W}{c_0} sowie am Ende des Experiments:
t_\mathrm{W(Wasser)}=\frac{s_\mathrm W}{c_\mathrm W}=\frac{s_\mathrm W}{c_0}n_\mathrm W
Einsetzen in die Formel für die Zeitdifferenz:
t_2 - t_1 =\frac{s_\mathrm W}{c_0}n_\mathrm W - \frac{s_\mathrm W}{c_0} = \frac{s_\mathrm W}{c_0}\left( n_\mathrm W -1 \right) = \frac{2\Delta h}{c_0}\left( n_\mathrm W -1 \right)
Umstellen liefert die Formel für die Brechzahl:
n_\mathrm W = 1+\frac{c_0}{2\Delta h}\left(t_2 - t_1 \right)
Mit den Zahlenwerten aus der Aufgabenstellung ergibt sich:
n_\mathrm W =1{,}37
