Nested and Recursive Macro Calls

III.11.7 Nested and Recursive Macro Calls

Macro bodies may also contain macro calls, and so may the bodies of those called macros, and so forth.
If a macro call is seen throughout the expansion of a macro, the assembler starts immediately with the expansion of the called macro. For this, its its expanded body lines are simply inserted into the expanded macro body of the calling macro, until the called macro is completely expanded. Then the expansion of the calling macro is continued with the body line following the nested macro call.

Example 1:

 INSIDE MACRO
	SUBB	A,R3
 ENDM

 OUTSIDE MACRO
	MOV	A,#42
	INSIDE
	MOV	R7,A
 ENDM

In the body of the macro OUTSIDE, the macro ISIDE is called. If OUTSIDE is called (and the list mode is set to $GENONLY), one gets something like the following expansion:

        Line  I  Addr  Code		Source

	  15+ 1  0000  74 2A		MOV	A,#42
	  17+ 2  0002  9B		SUBB	A,R3
	  18+ 1  0003  FF		MOV	R7,A

Since macro calls can be nested to any depth (while there is free memory), the macro expansion level is shown in the I-column of the list file. Since macro and include file levels can be nested in arbitrary sequence and depth, the nesting level is counted through all macro and include file levels regardless. For better distinction, the character following the global line number is ':' for include file levels, and '+' for macro levels.

If macros are calling themselves, one speaks of recursive macro calls. In this case, there must be some stop criterion, to prevent the macro of calling itself over and over until the assembler is running out of memory! Here again, conditional assembly is the solution:

Example 2:

The macro COUNTDOWN is to define 16-bit constants from 1 thru n in descending order in ROM. n can be passed to the macro as a parameter:

 COUNTDOWN MACRO DEPTH
  IF DEPTH GT 0
	DW	DEPTH
	COUNTDOWN %DEPTH-1
  ENDIF
 ENDM

If COUNTDOWN is called like this,

	COUNTDOWN 7

something like the following macro expansion results (in list mode $GENONLY/$CONDONLY):

	Line  I  Addr  Code		Source

	  16+ 1  0000  00 07		DW	7
	  19+ 2  0002  00 06		DW	6
	  22+ 3  0004  00 05		DW	5
	  25+ 4  0006  00 04		DW	4
	  28+ 5  0008  00 03		DW	3
	  31+ 6  000A  00 02		DW	2
	  34+ 7  000C  00 01		DW	1

After the Dark Ages, when the dust was settling and the sun broke through the gloom, computer science discovered the method of recursive programming. There was no doubt that this was the Solution!
And the computer scientists started to explain this to the students. But it seemed that the students didn't get it. They always complained that recursive calculation of n! is a silly example indeed.
All the scientists felt stronly that there was still something missing. After 10 more years of hard research work, they also found the Problem:

Example 3:

The Towers of Hanoi

There are three vertical sticks on the table. On stick 1 there are n discs with different diameters and a hole in the middle, the smallest disc on top, the biggest on the bottom.

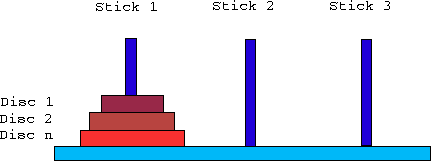
The Problem is to transfer the tower of discs from stick 1 to stick 2 with a minimum of moves. But only the topmost disc on a tower may be moved at one time, and no disc may be layed on a smaller disc. Stick 3 may be used for scratch purposes. This is a Solution with ASEM-51 macros:

	;The Towers of Hanoi

$GENONLY CONDONLY

DISCS	EQU	3	;number of discs

 HANOI MACRO n, SOURCE, DESTINATION, SCRATCH
  IF n > 0
	HANOI %(n-1), SOURCE, SCRATCH, DESTINATION
	;   move topmost disc from stick &SOURCE to stick &DESTINATION
	HANOI %(n-1), SCRATCH, DESTINATION, SOURCE
  ENDIF
 ENDM

	HANOI DISCS, 1, 2, 3

 END

The recursive macro HANOI generates an instruction manual for the Problem, where the instructions appear as comment lines in the list file. The symbol DISCS must be set to the desired number of discs. If HANOI is called like this,

	HANOI 3, 1, 2, 3

the following “instruction manual” is generated:

       27+ 3       ;   move topmost disc from stick 1 to stick 2
       35+ 2       ;   move topmost disc from stick 1 to stick 3
       44+ 3       ;   move topmost disc from stick 2 to stick 3
       53+ 1       ;   move topmost disc from stick 1 to stick 2
       64+ 3       ;   move topmost disc from stick 3 to stick 1
       72+ 2       ;   move topmost disc from stick 3 to stick 2
       81+ 3       ;   move topmost disc from stick 1 to stick 2

The GENONLY and CONDONLY controls ensure that the table doesn't contain all the macro calls and IF constructions.

Exercise 1:
Modify the macro HANOI so that it is generating a move table in ROM, which could directly be used as an input for an 8051-controlled robot-arm that really plays the game with 3 real sticks and n real discs.
Exercise 2:
Prove that the minimum number of moves is 2ⁿ - 1.