Division bei Mikrocontrollern

Betrachtet wird hier nur die Ganzzahldivision.

Grundlagen

Bei der Ganzzahldivision gilt folgende Regel der Bitbreiten:

Der unscheinbare (oder lästige) Rest ist übrigens oft sehr nützlich und fällt stets als Nebenprodukt mit an!
Hochsprachen verdecken (=verschenken!) die innewohnende Eigenschaft der Bitbreiten-Veränderung und des gleichzeitig anfallenden Divisionsrestes.

Es wird stets abgerundet (zur Null hin); zum Aufrunden vergleiche man den doppelten Rest mit dem Divisor, oder addiere vorher den halben Divisor auf den Dividenden.

Eine direkte Verarbeitung von Zweierkomplementzahlen ist unzweckmäßig und deshalb selten implementiert; deshalb vorher in Vorzeichen+Betrag umrechnen!

Hinweis (Moritz Strübe): Moderne Compiler können durch Optimierung:

• Bitbreitenveränderungen automatisch erfassen und kürzeren Kode generieren
• Div- und Mod-Operatoren mit den gleichen Operanden erkennen und zu einer Division zusammenfassen

Tipp: Bei der Division durch zu kleine Zahlen oder Null bekommt man als Ergebnis die größte darstellbare Zahl, bei allen Programmier-Varianten. Schutzverletzungen wie beim Mikroprozessor üblich muss man m. W. nicht beachten.
Die Überlaufsituation ist gegeben, wenn die oberen n bit des Dividenden größer oder gleich den n bit des Divisors ist.

Division durch [(kleine) Potenzen von] Zwei

Diese werden durch Rechtsschieben erledigt! — 1x Rechtsschieben = Division durch 2.
Dabei gibt es üblicherweise zwei Rechtsschiebebefehle, für vorzeichenlose und Zweierkomplement-Zahlen, sowie einen Rotationsbefehl für niederwertige Bytes. Begonnen wird, wie bei der schriftlichen Division, mit dem höchstwertigen Byte!

	mov	C,ACC.7
	rrc	a

	clr	C
	rrc	a

	rrc	a

	bcf	STATUS,C
	btfsc	R,7
	 bcs	STATUS,C
	rrf	R,f

	bcf	STATUS,C
	rrf	R,f

	rrf	R,f

	asr	R

	lsr	R

	ror	R

	ashr	R,#1

	shr	R,#1

	bmov	R.0,Rvorher.0
	ror	R,#1

Bei Potenzen von Zwei müssen die o.g. Befehle in einer Schleife ausgeführt werden.

Beachte: Alle, auch negative Zweierkomplementzahlen, werden stets abgerundet! Als Konsequenz erreicht man bei negativen Zahlen niemals Null, sondern maximal -1 (=0FFh als Byte gesehen).
Als Rest gilt das zuletzt herausgeschobene Bit.

Division durch [Potenzen von] 256 (=2⁸!)

Die Lösung dazu ist derartig trivial, dass sie oft nicht für voll genommen wird: Es wird byteweise „uminterpretiert“, bei gleich bleibender Bitbreite muss vorn ein Byte hinzugesetzt werden. Dieses Byte ist bei vorzeichenlosen Zahlen stets Null. Bei Zweierkomplement muss bei negativen Zahlen 0FFh aufgefüllt werden!

	mov	C,ACC.7	;a=altes MSB
	subb	a,ACC	;neues MSB

	clrf	R	;neues MSB
	btfsc	R,7	;R=altes MSB
	 decf	R,f	;neues MSB (0FFh)

	add	R,R	;R=altes MSB (wird zerstört)
	sbc	R,R	;neues MSB (0 oder 0FFh)

	movbs	R16,R8	;von 8 auf 16 Bits erweitern

	bmov	C,R16.15	;altes HI-Word MSB nach PSW.1
	subc	R16,R16	;neues HI-Word (0 oder 0FFFFh)

Beachte: Alle, auch negative Zweierkomplementzahlen, werden stets abgerundet!
Als Rest n bit gelten die „verworfenen“ Bytes.

Division durch „krumme“ Konstante via Multiplikation

Bisweilen ist ein Messwert o. ä. durch eine Skalierungskonstante zu dividieren. Dann ist es oftmals besser, mit einem 2ⁿfachen Kehrwert der Konstante zu multiplizieren und anschließend durch Rechtsschieben den Wert zu erhalten! Bei n=8 (oder =16) entfällt sogar das lästige Schieben.

Merke: Multiplizieren ist leichter als Dividieren!

Division mit eingebautem Divisionsbefehl

Dieser Fall erfordert ggf. das Umwandeln einer Zweierkomplement-Zahl in eine Vorzeichen-Betrags-Darstellung.
Voraussetzung für die Anwendbarkeit des eingebauten Befehls ist seine ausreichende Bitbreite:

	div	ab	

	divu	R

	divlu	R

	div	R

	divl	R

Division breiterer Zahlen mit eingebautem Divisionsbefehl

Dieser Fall der Kaskadierung ist bei Mikrocontrollern selten anzutreffen.

Zunächst benötigen Sie einen Divisionsbefehl mit den oben genannten Bitbreiten. Der 8051-Divisionsbefehl ist also nicht geeignet!

Weiterhin darf der Divisor die verfügbare Bitbreite nicht überschreiten! Ist der (bekannte!) Divisor zu groß, kann eine Primfaktorzerlegung zu einer mehrfach hintereinander ausführbaren Division führen, aber das ist meist nicht sinnvoll.

Merke: Kaskadierung ist für überlange Divisoren nicht möglich und erfordert stets die folgende Lösung.
Überlange Dividenden sind kein Problem.

Die Kaskadierung ist auch erforderlich, wenn nur der Quotient zu breit wird. Ggf. ist das High-Byte mit Null anzusetzen.

Beispiel (allgemein gehalten) für 16-bit-Quotient:

Division mit selbstgeschriebener Routine

Hierbei sind beliebige Bitbreiten realisierbar. Die übliche Routine dividiert 16 bit / 8 bit = 8 bit Rest 8 bit.

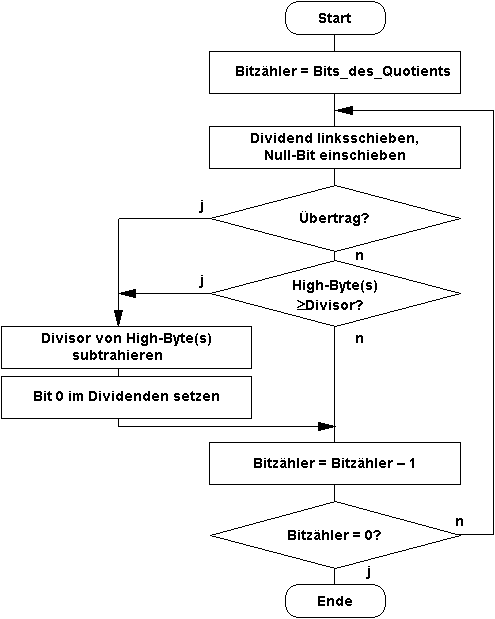
Die binäre Division erfolgt genauso wie die schriftliche Division; durch probeweise Subtraktion des (0-oder 1fachen des) Quotienten und Fortfahren zur nächsten Ziffer von links nach rechts.

Zweierkomplement-Zahlen müssen vorher nichtnegativ gemacht werden; das Vorzeichen des Quotienten ergibt sich aus der XOR-Verknüpfung der höchstwertigen Bits von Dividend und Divisor. Der Rest ist ohnhin nur für vorzeichenlose Zahlen definiert.

Anmerkung: Handgeschriebene Divisionen sind, wie oben angeführt, bei überlangen Divisoren immer vonnöten; auch auf Pentium u. ä. sind sie in der Laufzeitbibliothek von C bspw. für __int64-Ergebnisse enthalten!
Wegen der Verwandtschaft der Division zu Verschlüsselungs- und CRC-Routinen ist ihre Implementierung sehr ähnlich zu jenen Verfahren!

Beispiel: 12345 / 67 = 184 Rest 17 (3039h / 43h = 0B8h Rest 11h)

Denkmodell 1: Schriftliche Division

Denkmodell 2: Praktische Registeraufteilung für Mikrocontroller

Man beachte beim Subtraktionstest, dass ein vorher herausgeschobenes Übertragsbit auf jeden Fall eine Subtraktion erzwingt; das ist in diesem Beispiel nie der Fall.

Daraus ergibt sich, dass der Rest stets im High-Teil des Ergebnisses steht, auch beim eingebauten Divisionsbefehl ist das immer so!

Programmablaufplan

(Aufs Bild klicken für Original-Vektorgrafik)

Geplant sind downloadbare Makros für alle Mikrocontroller für alle Divisionen mit 8-bit- und 16-bit-Divisoren.

Zur Anwendung kommt die Division (meist durch 10) im Hornerschema zur Konvertierung einer (beliebig langen) Zahl in die ASCII-Repräsentation (entsprechend der C-Funktion itoa() oder innerhalb von printf()).
Zum Anzeigen von Zahlenwerten auf Displays kommt man daher kaum um die Division herum!