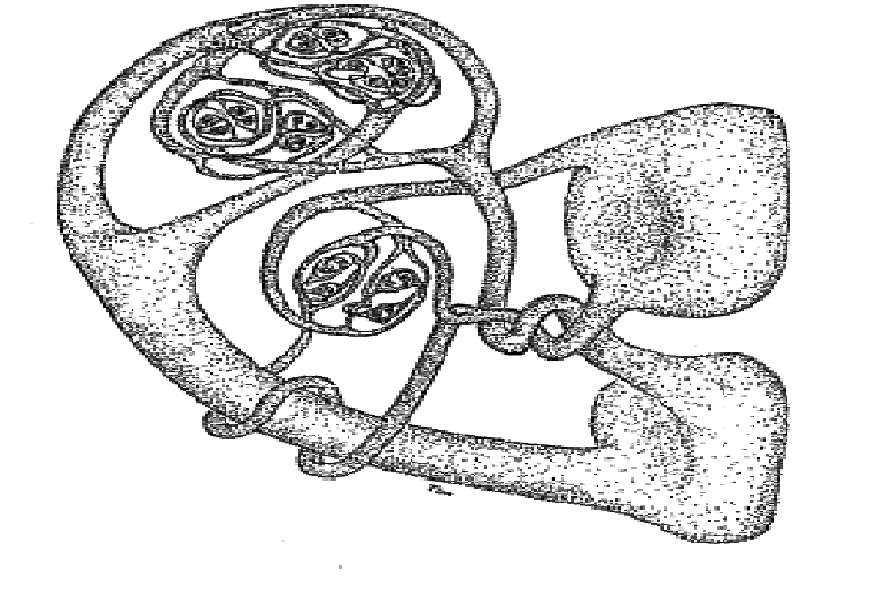
The Mating Dance of the Alexander Horned Spheres by Tim Poston
(from: http://www.math.ohio-state.edu/~fiedorow/math655/mating.html)
Ich halte im Sommersemester 2006 folgende Vorlesung (4V),
zu der alle Interessenten herzlich
eingeladen sind. Raum und
Zeit werden noch bekanntgegeben.
A. Böttcher
Ausgewählte Kapitel der Algebra, Analysis und Geometrie
oder
Eine Reise in die höhere Dimension
5. Die Alexandersche Sphäre
Das sollte man mal gesehen (und verstanden) haben.
6. Dreidimensionale Mannigfaltigkeiten
Dreimal die dreidimensionale Sphäre S^3, über das Verkleben
von Polyedern, Heegaard-Zerlegung
und Heegaard-Diagramme, Linsenräume, Dehn-Chirurgie.
7. Die Poincarésche Vermutung
und
andere Abgründe der Dimension
Homotopiegruppen, Gruppen mit definierenden Relationen, Wortproblem
und Isomorphie-
problem, Poincarésche Vermutung (bewiesen ab Dimension 4),
Homöomorphieproblem
für Mannigfaltigkeiten (unentscheidbar ab Dimension 4), Erkennung
der Sphäre (unentscheidbar
ab Dimension 5), Knotengruppen (Dehn, Papakyriakopoulos, Haken,
Waldhausen).
8. Differenzierbare Mannigfaltigkeiten
Differenzierbare Strukturen und Diffeomorphismen, Milnors
7-dimensionale
Sphären,
R^4 versus R^n, Einbettungen und Immersionen, und (wir lassen keine
Ungeheuerlichkeit aus)
über das Wenden einer Kugelfläche von innen nach außen.
9. Geometrie auf Mannigfaltigkeiten
Tangentialraum, metrischer Tensor, der sich ändernde Pythagoras,
die Sphären S^2 und S^3 als
Riemannsche Mannigfaltigkeiten.
10. Krümmungstensor und
Einsteinsche
Gleichungen
Gaußsche Krümmung von Flächen, Krümmungstensor,
Christoffelsymbole, Ricci-Tensor,
Krümmungsskalar, Minkowski-Raum, 4-dimensionale
Lorentz-Mannigfaltigkeiten,
Geodäten,
Grundpostulate der allgemeinen Relativitätstheorie und die
Einsteinschen
Gleichungen.
11. Schwarze Löcher
Schwarzschildlösung der Einsteinschen Gleichungen (mit allen
Rechendetails,
d.h., allgemeine
Relativitätstheorie ''zum Anfassen''), Schwarzschildradius, Reise
in ein schwarzes Loch,
Interpretation der ''Integrationskonstanten''.
12. Das Universum als Ganzes
Friedmannlösungen der Einsteinschen Gleichungen und deren
Interpretation:
sich ausdehnender
Euklidischer Raum, pulsierende dreidimensionale Sphäre (mit
''elliptischer''
Geometrie), und
sich ausdehnende dreidimensionale Pseudosphäre (mit hyperbolischer
= Lobatschewskischer
Geometrie).

The Mating Dance of the Alexander Horned Spheres by Tim Poston
(from: http://www.math.ohio-state.edu/~fiedorow/math655/mating.html)