Let AP(Sigma) be the Banach algebra generated by the functions
exp(i lambda x) (x in R) where lambda ranges over some additive
semigroup Sigma of nonnegative real numbers. The upper complex
half-plane C+ is a subset of the maximal ideal space of AP(Sigma).

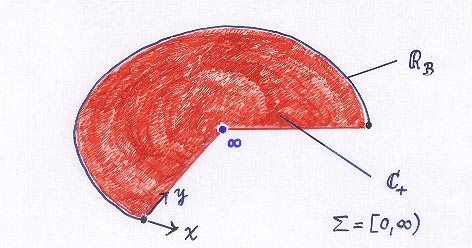
In the following case C+ is dense in the maximal ideal space, that is,
we have no corona:

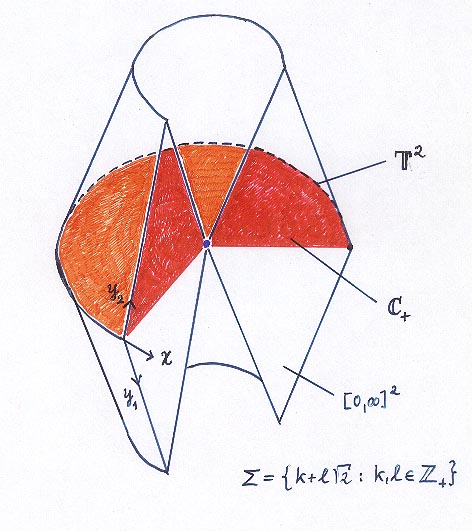
But here is a case where C+ is not dense in the maximal ideal space -
we may think of the maximal ideal space as a body of revolution and
of C+ as the equatorial plane of the body, which shows that the maximal
ideal space consists almost entirely of corona:

For more about this, see my paper No. 86.