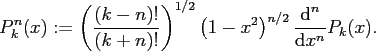Next: Spherical harmonics
Up: NFSFT - nonequispaced fast
Previous: Spherical coordinates
Contents
The Legendre polynomials
![$ P_k : [-1,1]\rightarrow \ensuremath{\mathbb{R}}$](img257.png) ,
, 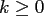 , as
classical orthogonal polynomials are given by their corresponding Rodrigues
formula
, as
classical orthogonal polynomials are given by their corresponding Rodrigues
formula
The associated Legendre functions
![$ P_k^n : [-1,1] \rightarrow \ensuremath{\mathbb{R}}$](img259.png) ,
,
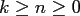 are defined by
are defined by
For 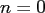 , they coincide with the Legendre polynomials
, they coincide with the Legendre polynomials
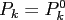 .
The associated Legendre functions
.
The associated Legendre functions 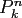 obey the three-term recurrence
relation
obey the three-term recurrence
relation
for
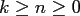 ,
,
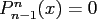 ,
,
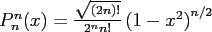 .
For fixed
.
For fixed 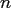 , the set
, the set
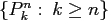 forms a set of
orthogonal functions, i.e.,
forms a set of
orthogonal functions, i.e.,
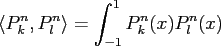 d d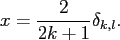 |
|
Again, we denote by
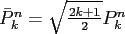 the
orthonormal associated Legendre functions.
In the following, we allow also for
the
orthonormal associated Legendre functions.
In the following, we allow also for 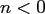 and set
and set 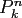 :=
:=
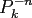 in this case.
in this case.




Next: Spherical harmonics
Up: NFSFT - nonequispaced fast
Previous: Spherical coordinates
Contents
Jens Keiner
2006-11-20
![]() ,
,
![]() are defined by
are defined by